images
images listlengths 0
7
| problem
stringlengths 14
1.49k
| answer
stringclasses 176
values |
|---|---|---|
质点在 $x O y$ 平面内作曲线运动,则质点速率的正确表达式为( )。
A.$v=\frac{\mathrm{d} r}{\mathrm{~d} t}$
B.$v=\frac{\mathrm{d}|\boldsymbol{r}|}{\mathrm{d} t}$
C.$v=\left|\frac{\mathrm{d} \boldsymbol{r}}{\mathrm{d} t}\right|$
D.$v=\frac{\mathrm{d} s}{\mathrm{~d} t}$
E.$v=\sqrt{\left(\frac{\mathrm{d} x}{\mathrm{~d} t}\right)^{2}+\left(\frac{\mathrm{d} y}{\mathrm{~d} t}\right)^{2}}$
|
B
|
|
质点作匀速圆周运动,下列各量中恒定不变的量是 ( )。
A. $\lim _{\Delta t \rightarrow 0} \frac{\Delta r}{\Delta t}$
B. $\lim _{\Delta t \rightarrow 0} \frac{\Delta r}{\Delta t}$
C. $\lim _{\Delta r \rightarrow 0} \frac{|\Delta r|}{\Delta t}$
D. $\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t}$
E. $\lim _{\Delta t \rightarrow 0} \frac{\Delta v}{\Delta t}$
F. $\lim _{\Delta t \rightarrow 0} \frac{|\Delta| \nu}{\Delta t}$
|
C
|
|
下列表述中正确的是()。
A.质点沿 $x$ 轴运动,若加速度 $a<0$ ,则质点必作减速运动。
B.在曲线运动中,质点的加速度必定不为零。
C.若质点的加速度为恒矢量,则其运动轨道必为直线。
D.当质点作抛体运动时,其法向加速度 $a_{n}$ 、切向加速度 $a_{t}$ 是不断变化的,因此 $a=\sqrt{a_{n}^{2}+a_{t}^{2}}$ 也是不断变化的。
|
C
|
|
在离水面高度为 $h$ 的湖岸边上,有人用绳子拉船靠岸。若人以匀速率 $v_{0}$ 收绳,则船在水中的运动为()。
A.匀速运动,且 $v=v_{0}$
B.加速运动,且 $v>v_{0}$
C.加速运动,且 $v<v_{0}$
D.减速运动。
|
B
|
|
已知质点的运动方程为 $\left\{\begin{array}{l}x=A t \cos \theta+B t^{2} \cos \theta \\ y=A t \sin \theta+B t^{2} \sin \theta\end{array}\right.$ 式中 $A, B, \theta$ 均为恒量,且 $A>0, B >0$ ,则质点的运动为()。
A.一般曲线运动
B.匀速直线运动
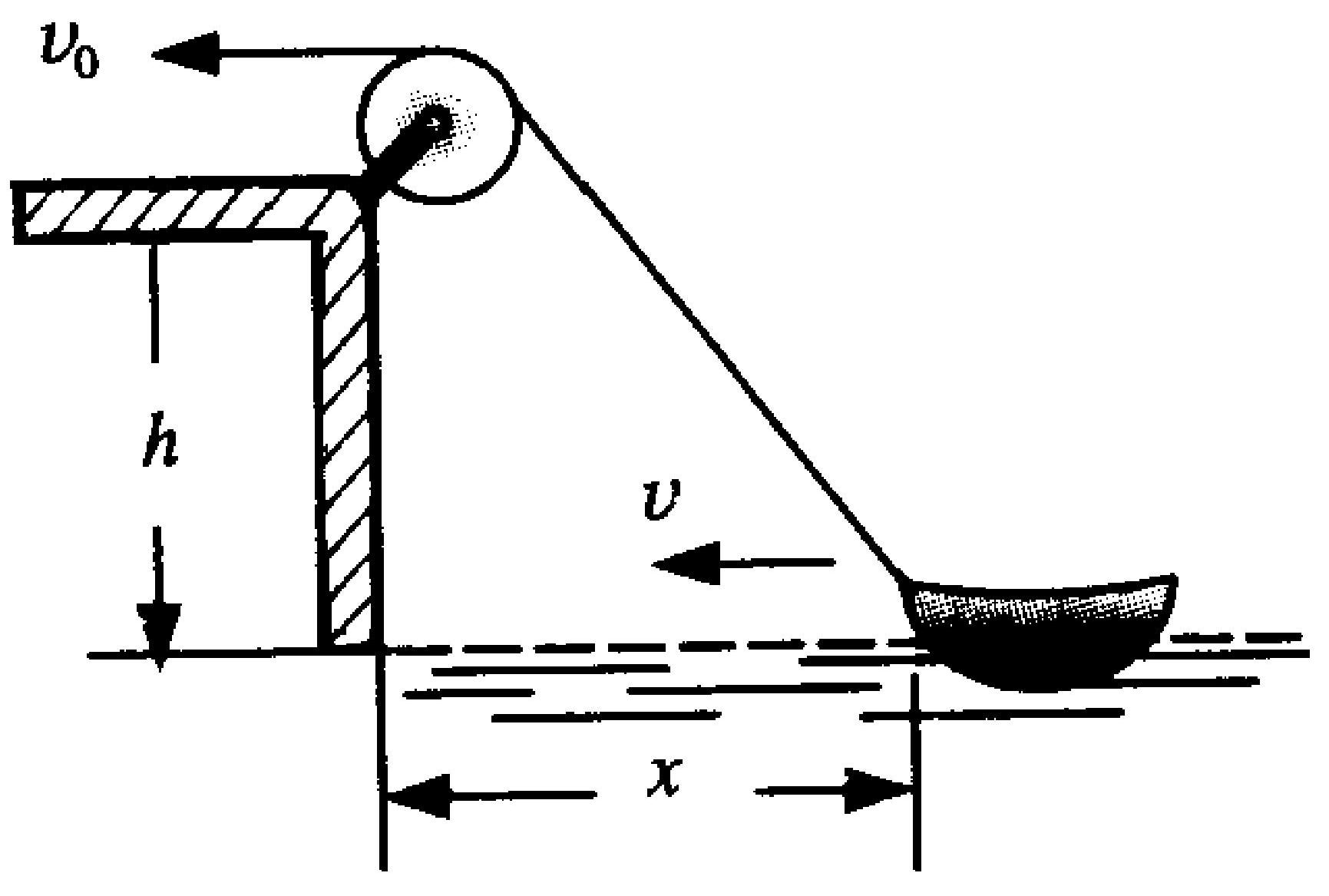
图 1-1
C.圆周运动
D.匀减速直线运动
E.椭圆运动 F.匀加速直线运动
|
C
|
|
下列说法中正确的是()。
A.作曲线运动的物体,必有切向加速度
B.作曲线运动的物体,必有法向加速度
C.具有加速度的物体,其速率必随时间改变
|
C
|
|
在相对地面静止的坐标系内,$A, B$ 两船都以 $2 \mathrm{~m} \cdot \mathrm{~s}^{-1}$ 的速率匀速行驶,$A$ 船沿 $x$ 轴正向,$B$ 船沿 $y$ 轴正向。今在 $A$ 船上设置与静止坐标系方向相同的坐标系( $x, y$ 方向的单位矢量用 $i, j$ 表示),那么在 $A$ 船上的坐标系中,$B$ 船的速度(以 $\mathrm{m} \cdot \mathrm{s}^{-1}$ 为单位)为 ( )。
A. $2 i+2 j$
B.$-2 \boldsymbol{i}+2 \boldsymbol{j}$
C.$-2 \boldsymbol{i}-2 \boldsymbol{j}$
D. $2 i-2 j$
|
A
|
|
下列各种情况中,不可能存在的是()。
A.速率增加,加速度减小
B.速率减小,加速度增大
C.速率不变而有加速度
D.速率增大而无加速度
E.速率增大,而法向加速度的大小不变
|
D
|
|
一物体作单向直线运动,它在通过两个连续相等位移的平均速度分别为 $\bar{v}_{1}=10 \mathrm{~m} \cdot \mathrm{~s}^{-1}, ~ \bar{v}_{2}=15 \mathrm{~m} \cdot \mathrm{~s}^{-1}$ 。则在整个过程中该物体的平均速度为()。
A. $12.5 \mathrm{~m} \cdot \mathrm{~s}^{-1}$
B. $11.75 \mathrm{~m} \cdot \mathrm{~s}^{-1}$
C. $12 \mathrm{~m} \cdot \mathrm{~s}^{-1}$
D. $13.75 \mathrm{~m} \cdot \mathrm{~s}^{-1}$
|
B
|
|
下列表述中正确的是()。
A.内力作用对系统的动量没有影响
B.内力不能改变系统的总动量
C.内力不能改变系统的总动能
D.内力对系统做功的总和不一定为零
|
B
|
|
下列表述中正确的是()。
A.外力作功的代数和为零,则系统的动量守恒
B.系统所受合外力恒等于零,则动量守恒
C.系统所受合外力冲量的矢量和为零,则动量守恒
D.动量守恒定律仅适用于惯性参照系,但与惯性系的选择无关
|
C
|
|
如图 2-1 所示,劲度系数为 $k$ 的轻弹簧水平放置,一端固定,另一端系一质量为 $m$ 的物体,物体与水平面间的摩擦系数为 $\mu$ 。开始时,弹簧没有伸长,现以恒力 $F$ 将物体自平衡位置开始向右拉动,则系统的
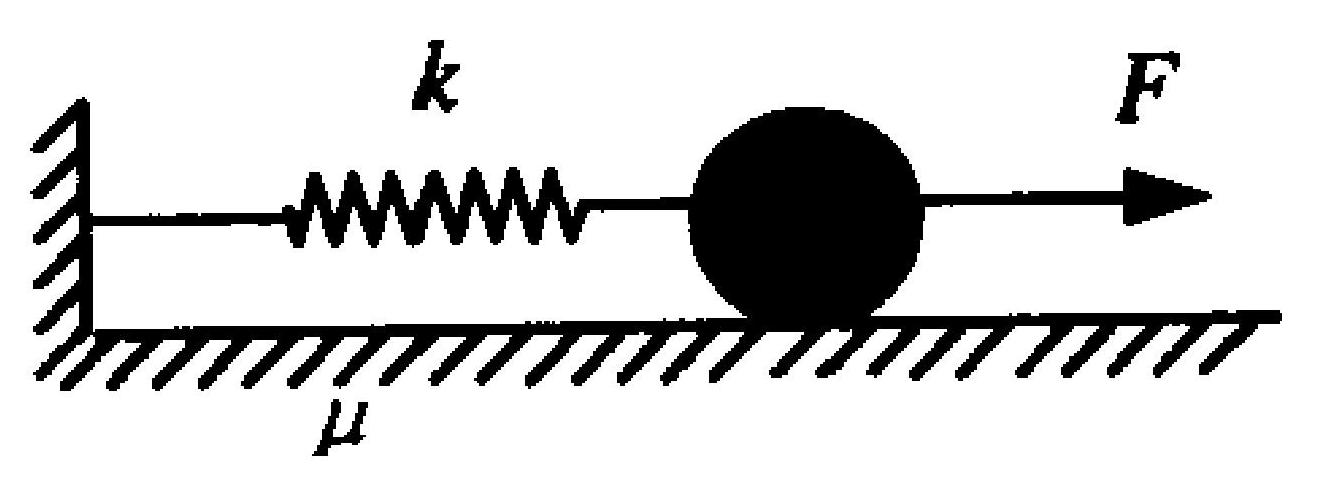
图 2-1
最大势能为 。
A.$\frac{2}{k}(F-\mu m g)^{2}$
B.$\frac{1}{2 k}(F-\mu m g)^{2}$
C.$\frac{2}{k} F^{2}$
D.$\frac{1}{2 k} F^{2}$
|
C
|
|
我国第一颗人造卫星绕地球作椭圆运动,地球中心为椭圆
的一个焦点。在运行过程中,下列叙述中正确的是
A.动量守恒
B.动能守恒
C.角动量守恒
D.以上均不守恒
|
B
|
|
如图2-2所示,在水平光滑的圆盘上,有一质量为 $m$ 的质点,拴在一根穿过圆盘中心光滑小孔的轻绳上。开始时质点离中心的距离为 $r$ ,并以角速度 $\omega$ 转动。今以均匀速度向下拉绳,将质点拉至离中心 $r / 2$ 处时,拉力所作的功为
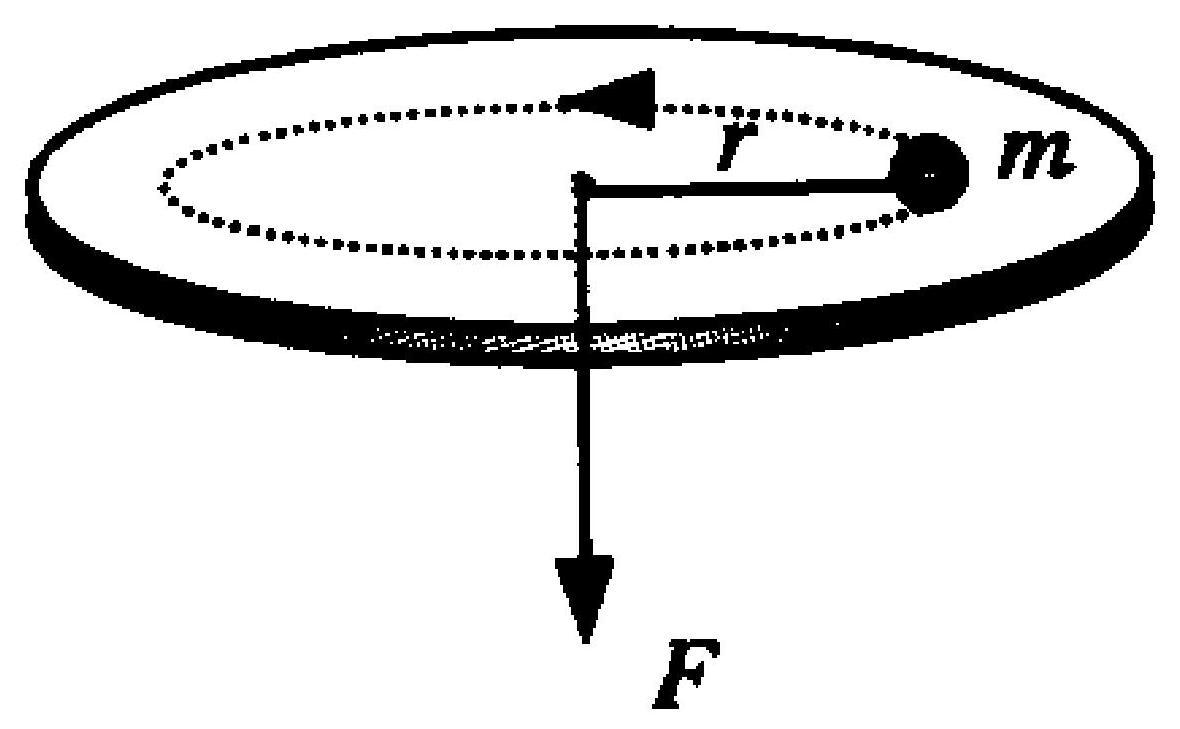
图 2-2
A.$\frac{1}{2} m r^{2} \omega^{2}$
B.$\frac{3}{2} m r^{2} \omega^{2}$
C.$\frac{5}{2} m r^{2} \omega^{2}$
D.$\frac{7}{2} m r^{2} \omega^{2}$
|
C
|
|
一力学系统由两个质点组成,它们之间只有引力作用。若两质点所受外力的矢量和为零,由此系统
A.动量、机械能以及对一轴的角动量守恒。
B.动量、机械能守恒,但角动量是否守恒不能断定。
C.动量守恒,但机械能和角动量是否守恒不能断定。
D.动量和角动量守恒,但机械能是否守恒不能断定。
|
C
|
|
对于一对作用力和反作用力来说,二者持续时间相同。下列结论中正确的是
A.二者做功必相同。
B.二者做功总是大小相等符号相反。
C.二者的冲量相同。
D.二者冲量不同,做功也不一定相等。
|
A
|
|
已知地球的质量为 $m$ ,太阳的质量为 $M$ ,地心与日心的距离为 $R$ ,引力常数为 $G$ ,则地球绕太阳作圆周运动的轨道角动量为

A.$m \sqrt{G M R}$
B.$\sqrt{\frac{G M m}{R}}$
C.$m M \sqrt{\frac{G}{R}}$
D.$\sqrt{\frac{G M m}{2 R}}$
|
D
|
|
如图2-3所示,一质量为 $m$ 的物体,位于质量可以忽略的直立弹簧正上方高度为 $h$ 处,该物体从静止开始落向弹黄。若弹簧的劲度系数为 $k$ ,不考虑空气阻力,则物体可能获得的最大动能是
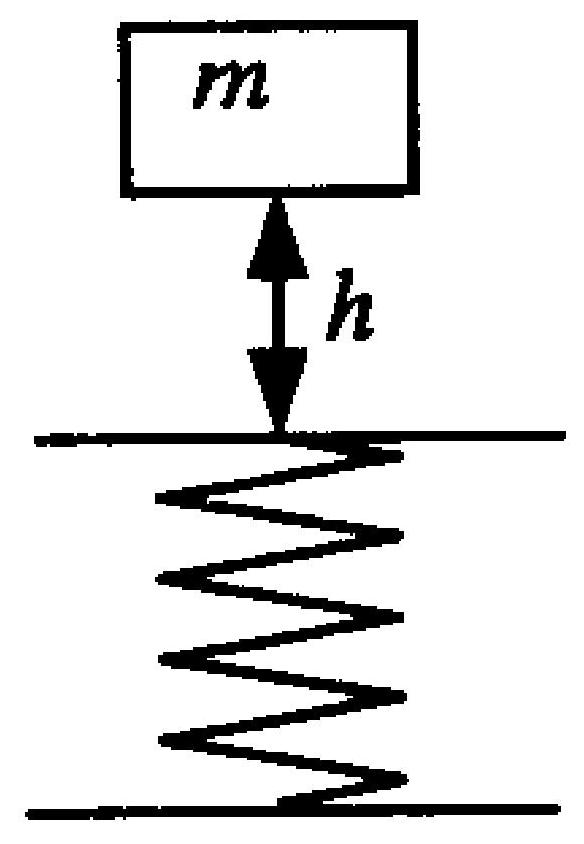
图 2-3
A.$m g h$
B.$m g h-\frac{m^{2} g^{2}}{2 k}$
C.$m g h+\frac{m^{2} g^{2}}{2 k}$
D.$m g h+\frac{m^{2} g^{2}}{k}$
|
B
|
|
有些矢量是相对于一定点(或轴)而确定的,有些矢量是与定点(或轴)的选择无关的。下列给出的各量中,相对于定点(或轴)而确定的物理量是()。
A.矢径
B.位移
C.速度
D.动量
E.角动量
F.力
G.力矩
|
B
|
|
某刚体绕定轴作匀变速转动时,对于刚体上距转轴为 $r$ 处的任一质元 $\Delta m$ 来说,它的法向加速度和切向加速度分别用 $a_{n}$ 和 $a_{t}$ 来表示,则下列表述中正确的是()。
A.$a_{n}, a_{t}$ 的大小均随时间变化
B.$a_{n}$ 和 $a_{t}$ 的大小均保持不变
C.$a_{n}$ 的大小变化,$a_{t}$ 的大小恒定不变
D.$a_{n}$ 的大小保持恒定,$a_{t}$ 的大小变化
|
C
|
|
工程技术上的摩擦离合器是通过摩擦实现传动的装置,其结构如图3-1所示。轴向作用力可以使 A,B 两个飞轮实现离合。当 A 轮与 B 轮接合通过摩擦力矩带动 B 轮转
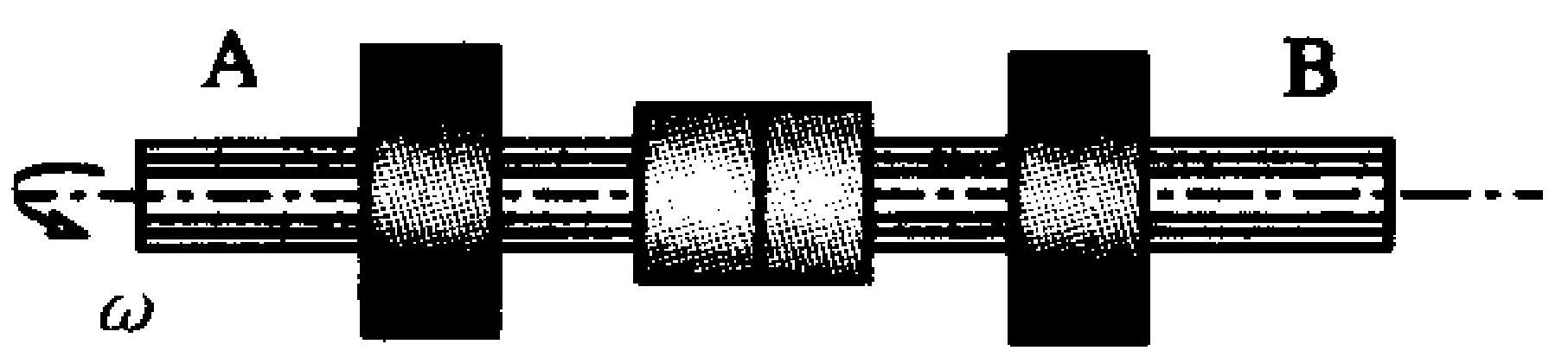
图 3-1
动时,则此刚体系统在两轮接合前后 。
A.角动量改变,动能亦改变
B.角动量改变,动能不变
C.角动量不变,动能改变
D.角动量不变,动能亦不改变
|
C
|
|
一人张开双臂手握哑铃坐在转椅上,让转椅转动起来,若此后无外力矩作用,则当此人收回双臂时,人和转椅这一系统的 ( )
A.转速加大,转动动能不变
B.角动量加大
C.转速和转动动能都加大
D.角动量保持不变
|
B
|
|
有 $a, b$ 两个半径相同,质量相同的细圆环,其中 $a$ 环的质量均匀分布,而 $b$ 环的质量分布不均匀,若两环对过环心且与环面垂直轴的转动惯量分别为 $I_{a}$ 和 $I_{b}$ ,则( )。
A.$I_{a}>I_{b}$
B.$I_{a}<I_{b}$
C.$I_{a}=I_{b}$
D.无法确定 $I_{a}$ 与 $I_{b}$ 的相对大小
|
C
|
|
下列说法中正确的是()。
A.系统的动量守恒,它的角动量也一定守恒
B.系统的角动量守恒,它的动量也必定守恒
C.系统的角动量守恒,它的机械能也一定守恒
D.以上表述均不正确
|
C
|
|
如图3-2所示,一悬线长为 $l$ ,质量为 $m$ 的单摆和一长度为 $l$ 、质量为 $m$ 能绕水平轴自由转动的匀质细棒,现将摆球和细棒同时从与竖直方向成 $\theta$ 角的位置由静止释放,当它们运动到竖直位置时,摆球和细棒的角速度

图 3-2
之间的关系为( )。
A.$\omega_{1}>\omega_{2}$
B.$\omega_{1}=\omega_{2}$
C.$\omega_{1}<\omega_{2}$
|
A
|
|
如图 3-3 所示,圆盘绕轴 $O$ 转动,若同时对称地射来两颗
质量相同,速度大小相同,方向相反且沿同一直线运动的子弹。射人后两颗子弹均留在盘内,则子弹射入后圆盘的角速度 $\omega$ 将
。
A.增大
B.不变
C.减少
D.无法判断
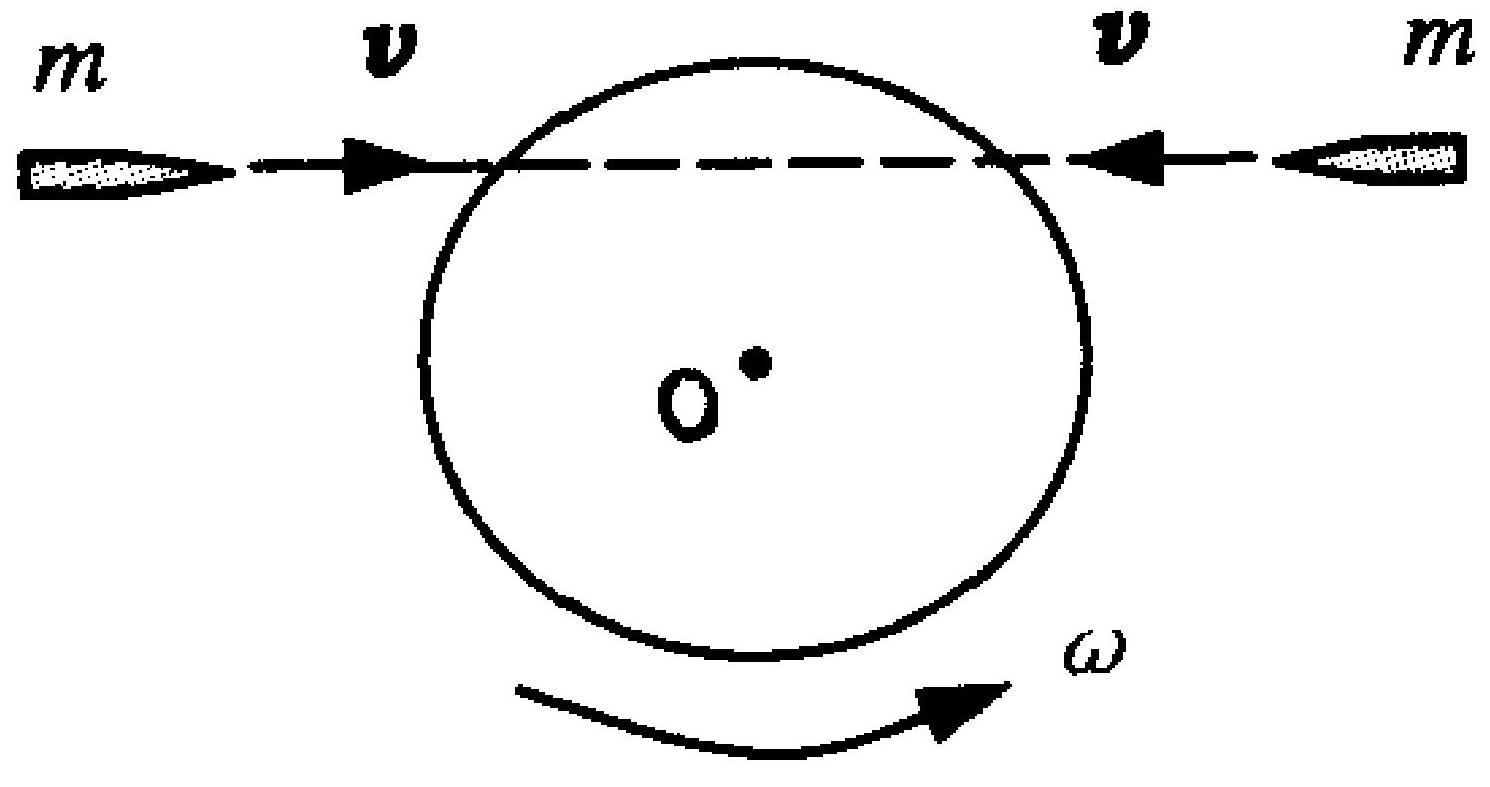
图 3-3
|
D
|
|
如图 4-1 所示,在坐标 $(a, o)$ 处放置一点电荷 $+q$ ,在坐标 $(-a, o)$ 处放置另一点电荷 $-q, \mathrm{P}$点是 $x$ 轴上的任一点,坐标为 $(x$ , $o)$ 。当 $x \gg a$ 时, P 点场强 $\boldsymbol{E}$ 的大小为( )
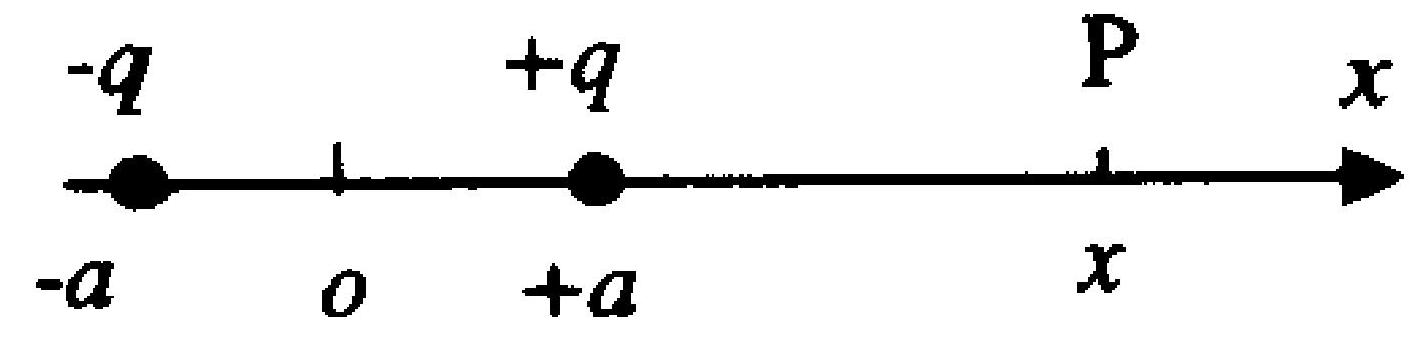
。
A.$\frac{q}{4 \pi \varepsilon_{0} x}$
B.$\frac{q a}{\pi \varepsilon_{0} x^{3}}$
C.$\frac{q a}{2 \pi \varepsilon_{0} x^{3}}$
D.$\frac{q}{4 \pi \varepsilon_{0} x^{2}}$
|
B
|
|
如图 4-2 所示,半径为 $R$ 的半球面置于电场强度为 $\boldsymbol{E}$ 的均匀电场中,选半球面的外法线为面法线正方 向,则通过该半球面的电场强度通量 $\Phi_{E}$为 。
A.$\pi R^{2} E$
B. 0
C. $3 \pi R^{2} E$
D.$-\pi R^{2} E$
E.$-2 \pi R^{2} E$
|
C
|
|
在静电场中,高斯定理告诉我们
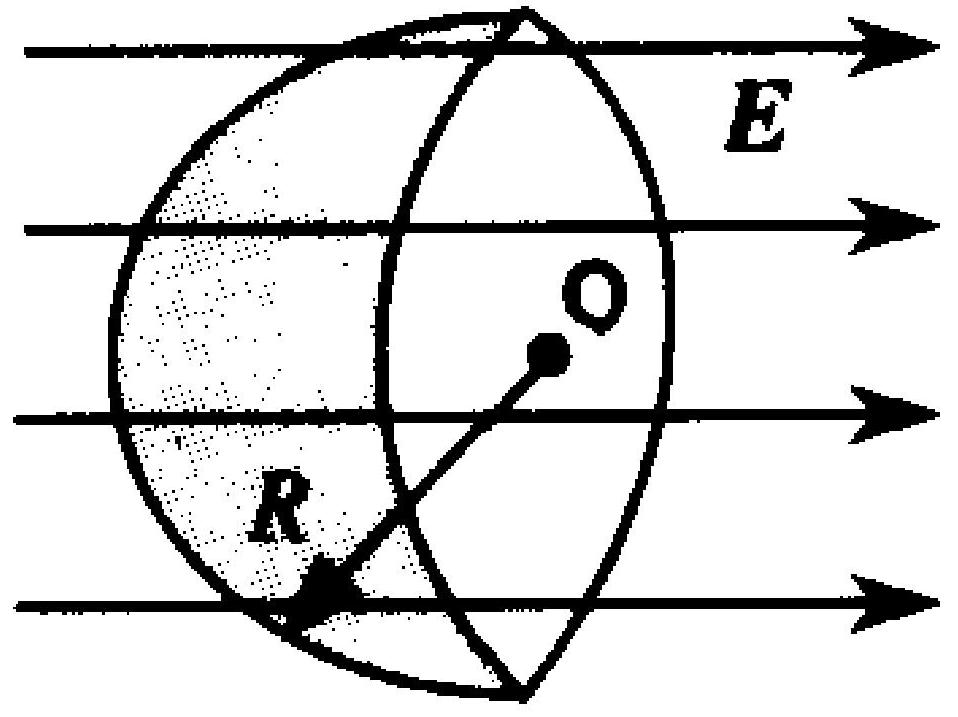
图 4-2
。
A.高斯面内不包围电荷,则面上各点 $\boldsymbol{E}$ 的量值处处为零
B.高斯面上各点的 $\boldsymbol{E}$ 只与面内电荷有关,与面外电荷无关
C.穿过高斯面的 $\boldsymbol{E}$ 通量,与面内电荷有关,但与面内电荷分布无关
D.穿过高斯面的 $\boldsymbol{E}$ 通量为零,则面上各点的 $\boldsymbol{E}$ 必为零
|
C
|
|
图4-3中所示为一沿 $x$ 轴放置的"无限长"分段均匀带电直线,电荷线密度分别为 $+\lambda(x <0$ 处 $)$ 和 $-\lambda(x>0$ 处 $)$ ,则 $O x y$ 坐标面上 P 点 $(0, a)$ 处的场强 $\boldsymbol{E}$ 为 。
A.$\frac{\lambda}{2 \pi \varepsilon_{0} a} i$
B.$\frac{\lambda}{4 \pi \varepsilon_{0} a} \boldsymbol{i}$
C.$\frac{\lambda}{4 \pi \varepsilon_{0} a}(i+j)$
D. 0
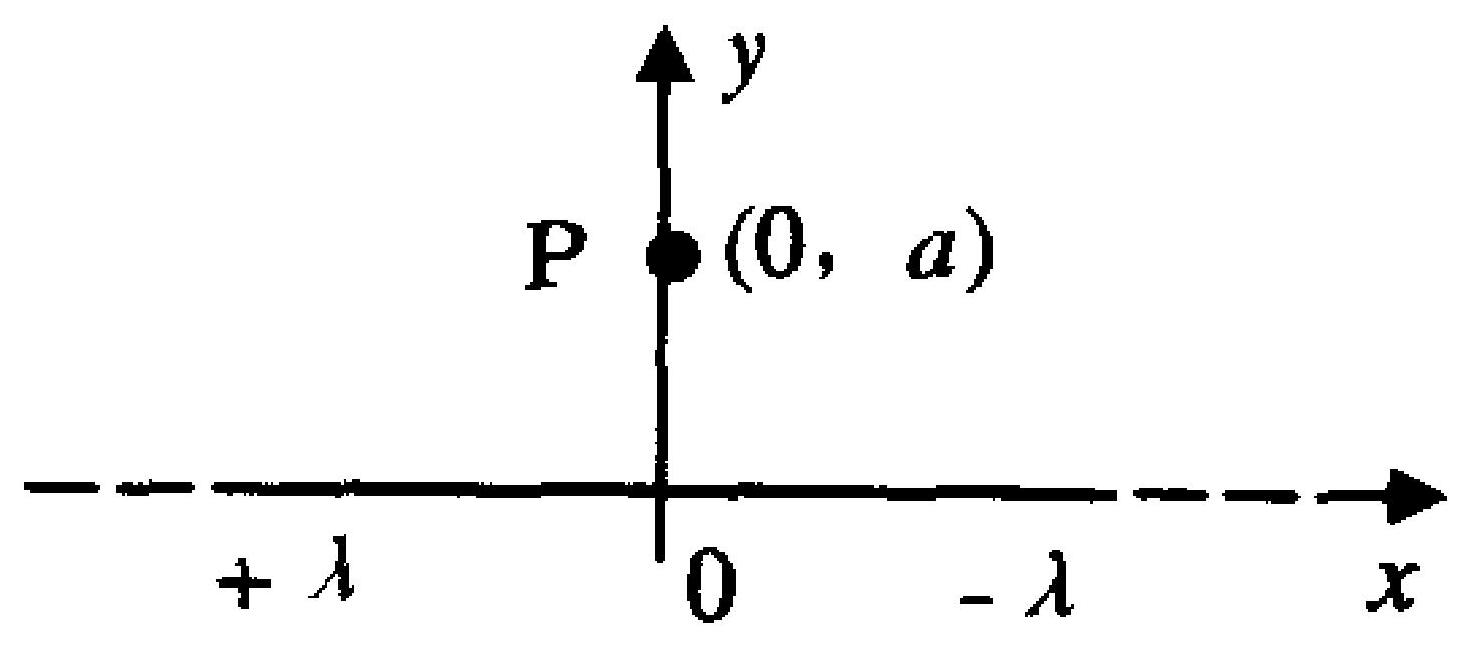
图4-3
|
B
|
|
两块平行平板,相距 $d$ ,板面积均为 $S$ ,分别均匀带电 $+q$ 和 $-q$ ,若两板的线度远大于 $d$ ,则它们的相互作用力的大小为
。
A.$\frac{q^{2}}{4 \pi \varepsilon_{0} d^{2}}$
B.$\frac{q^{2}}{\varepsilon_{0} S}$
C.$\frac{q^{2}}{2 \varepsilon_{0} S}$
D.$\infty$
|
C
|
|
下列说法中,正确的是 。
A.初速度为零的点电荷置于静电场中,将一定沿一条电场线运动
B.带负电的点电荷,在电场中从 a 点移到 b 点,若电场力作正功,则 $\mathrm{a}, \mathrm{b}$ 两点的电势关系为 $U_{\mathrm{a}}>U_{\mathrm{b}}$
C.由点电荷电势公式 $U=q / 4 \pi \varepsilon_{0} r$ 可知,当 $r \rightarrow 0$ 时,则 $U \rightarrow \infty$
D.在点电荷的电场中,离场源电荷越远的点,其电势就越低
E.在点电荷的电场中,离场源电荷越远的点,电场强度的量值就越小
|
C
|
|
半径为 $R_{1}, R_{2}$ 的同心球面上,分别均匀带电 $q_{1}$ 和 $q_{2}$ ,其中 $R_{2}$ 为外球面半径,$q_{2}$ 为外球面所带电荷量,设两球面的电势差为 $\Delta U$ ,则 。
A.$\Delta U$ 随 $q_{1}$ 的增加而增加。
B.$\Delta U$ 随 $q_{2}$ 的增加而增加。
C.$\Delta U$ 不随 $q_{1}$ 的增减而改变。
D.$\Delta U$ 不随 $q_{2}$ 的增减而改变。
|
A
|
|
如图 4-4 所示,两无限大平行平板,其电荷面密度均为 $+\sigma$ ,图中 $\mathrm{a}, \mathrm{b}, \mathrm{c}$ 三处的电场强度的大小分别为 。
A. $0, \quad \frac{\sigma}{\varepsilon_{0}}, \quad 0$
B.$\frac{\sigma}{\varepsilon_{0}}, \quad 0, \quad \frac{\sigma}{\varepsilon_{0}}$
C.$\frac{\sigma}{2 \varepsilon_{0}}, \quad \frac{\sigma}{\varepsilon_{0}}, \quad \frac{\sigma}{2 \varepsilon_{0}}$
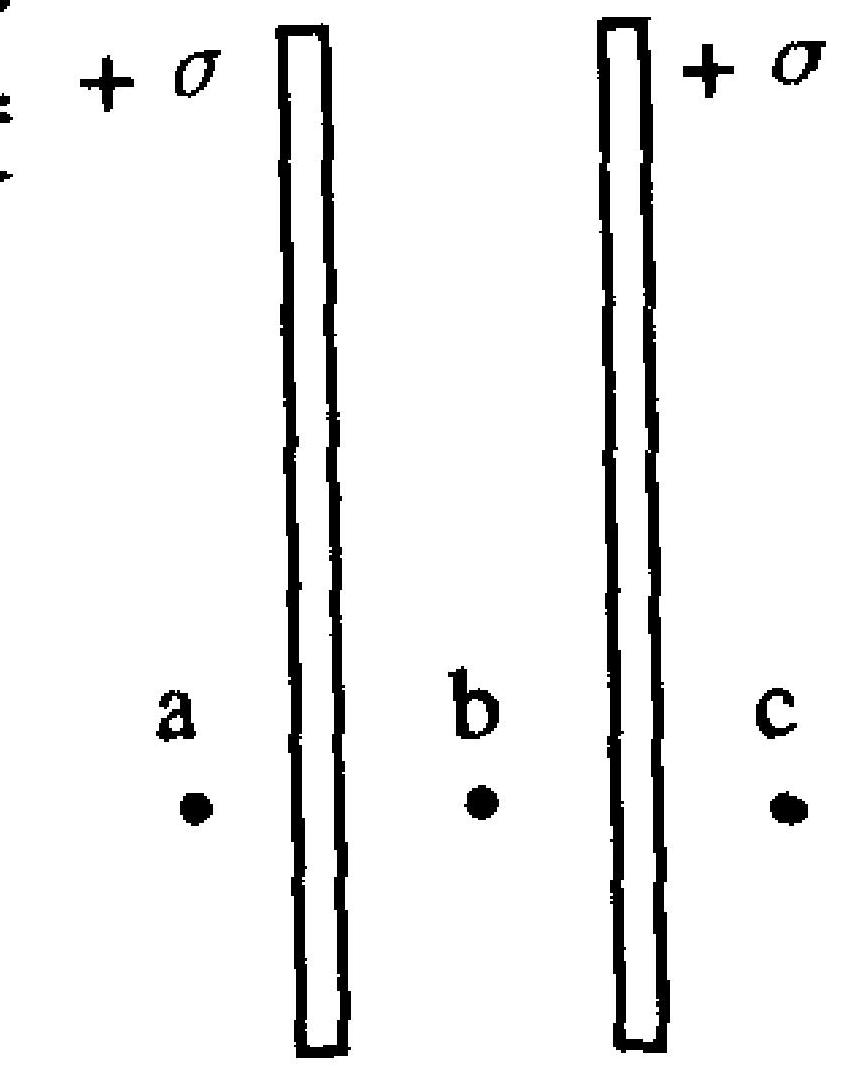
图 4-4
D. $0, \quad \frac{\sigma}{2 \varepsilon_{0}}, \quad 0$
|
D
|
|
某区域静电场的电场线分布情况如图4-5所示,一负电荷从 $M$ 点移到 $N$ 点,有人根据此图得出下列几点结论,其中哪点是正确的?
A.电场强度 $E_{\mathrm{M}}>E_{\mathrm{N}}$ ,电场力做正功;
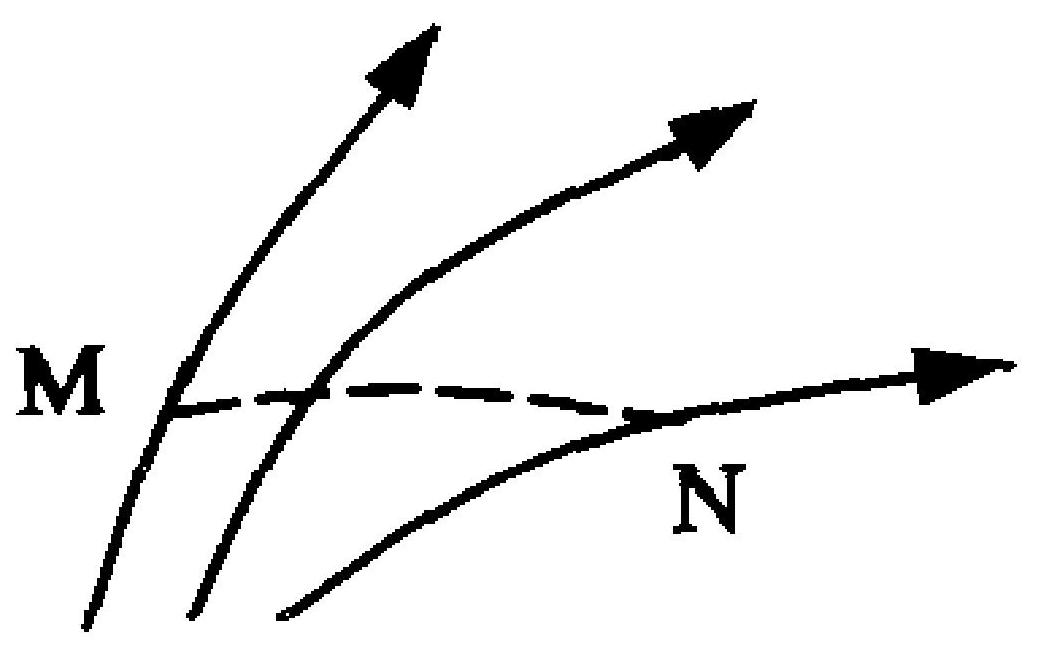
图 4-5
B.电势 $U_{\mathrm{M}}<U_{\mathrm{N}}$ ,电场力做负功;
C.电势能 $W_{\mathrm{M}}<W_{\mathrm{N}}$ ,电场力做负功;
D.负电荷电势能增加,电场力做正功。
|
B
|
|
在静电场中,下列说法正确的是 。
A.电场强度 $E=0$ 的点,电势也一定为零
B.同一条电场线上各点的电势不可能相等
C.在电场强度相等的空间内,电势也处处相等
D.在电势相等的三维空间内,电场强度处处为零
| ||
在静电场中,下列说法正确的是()。
A.带正电荷的导体,其电势一定是正值
B.等势面上各点的场强一定相等
C.在导体表面附近处的场强,是由该表面上的电荷 $\sigma$ 产生的,与空间其它地方的电荷无关
D.一个孤立的带电导体,表面的曲率半径愈大处,电荷密度愈小
|
B
|
|
在一个不带电的导体球壳的球心处放人一点电荷 $q$ ,当 $q$ 由球心处移开,但仍在球壳内时,请判断()。
A.球壳内、外表面的感应电荷均不再均匀分布
B.球壳内表面感应电荷分布不均匀,外表面感应电荷分布均匀
C.球壳内表面感应电荷分布均匀,外表面感应电荷分布不均匀
D.球壳内、外表面感应电荷仍保持均匀分布
|
C
|
|
如图5-1所示,一无限大均匀带电平面附近放置一与之平行的无限大导体平板。已知带电平面的电荷面密度为 $\sigma$ ,导体板两表面1和2的感应电荷面密度为()。
A.$\sigma_{1}=-\sigma, \quad \sigma_{2}=+\sigma$
B.$\sigma_{1}=-\frac{\sigma}{2}, \sigma_{2}=\frac{\sigma}{2}$
C.$\sigma_{1}=+\sigma, \quad \sigma_{2}=-\sigma$
D.$\sigma_{1}=+\frac{\sigma}{2}, \quad \sigma_{2}=-\sigma$
|
C
|
|
带电体外套一导体球壳,则下列说法中正确的是()。
A.壳外电场不影响壳内电场,但壳内电场要影响壳外电场
B.壳内电场不影响壳外电场,但壳外电场要影响
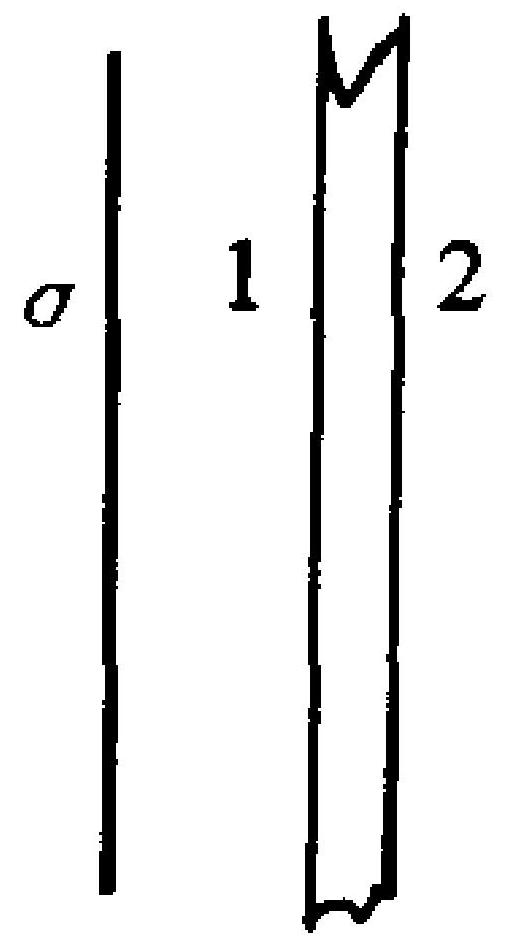
图5-1
壳内电场
C.壳内、外电场互不影响
D.壳内、外电场仍互相影响
E.若将外球壳接地,则答案 C 是正确的。
|
B
|
|
如图5-2所示,两同心金属球壳,它们离地球很远。如果外球壳上带正电 $q$ ,当内球壳用细导线穿过外球壳上的绝缘小孔与地连接,则内球壳( )。
A.不带电荷
B.带正电荷
C.带负电荷
D.球壳外表面带负电荷,内表面带等量正电荷
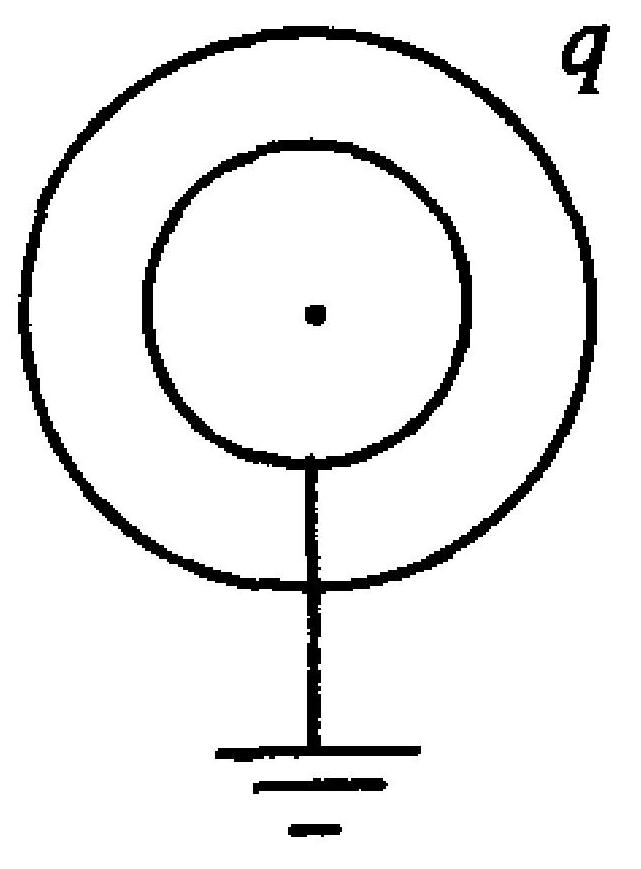
图 5-2
|
C
|
|
关于高斯定理,下列说法中正确的是 ( )
A.高斯面内不包围自由电荷,则穿过高斯面的 $\boldsymbol{D}$ 通量与 $\boldsymbol{E}$ 通量均为零
B.高斯面上的 $\boldsymbol{D}$ 处处为零,则面内自由电荷的代数和必为零
C.高斯面上各点 $D$ 仅由面内自由电荷决定
D.穿过高斯面的 $\boldsymbol{D}$ 通量仅与面内自由电荷有关,而穿过高斯面的 $E$ 通量与高斯面内外的自由电荷均有关
|
C
|
|
一平行板电容器与电源相连,电源端电压 $U$ ,电容器极板间距离为 $d$ ,电容器中充满两块大小相同,介电常数分别为 $\varepsilon_{1}$ 和 $\varepsilon_{2}$ 的均匀电介质板,如图5-3所示,则左、右两侧电介质中的电位移 $\boldsymbol{D}$的大小分别为 。
A.$D_{1}=D_{2}=\frac{\varepsilon_{0} U}{d}$
B.$D_{1}=\frac{\varepsilon_{1} U}{d}, \quad D_{2}=\frac{\varepsilon_{2} U}{d}$
C.$D_{1}=\frac{\varepsilon_{0} \varepsilon_{1} U}{d}, \quad D_{2}=\frac{\varepsilon_{0} \varepsilon_{2} U}{d}$
D.$\dot{D}_{1}=\frac{U}{\varepsilon_{1} d}, \quad D_{2}=\frac{U}{\varepsilon_{2} d}$

图 5-3
|
A
|
|
一空气平行板电容器充电后与电源断开,然后在两极板间充满各向同性均匀电介质,则场强的大小 $E$ 、电容 $C$ 、电压 $U$ 、电场能量 $W$ 。四个量各自与充入介质前相比较,增大(用 $\uparrow$ 表示)或减小(用 $\downarrow$ 表示)的情形为 。
A.$E \downarrow, C \uparrow, U \uparrow, W, \downarrow$
B.$E \uparrow, C \downarrow, U \downarrow, W . \uparrow$
C.$E \uparrow, C \uparrow, U \uparrow, W, \uparrow$
D.$E \downarrow, C \uparrow, U \downarrow, W . \downarrow$
|
D
|
|
一内外半径分别为 $R_{1}$ 和 $R_{2}$ 的同心球形电容器,其间充满相对介电常数为 $\varepsilon_{r}$ 的电介质,当内球带电量为 $Q$ 时,电容器中的储能为 。
A.$W_{e}=\frac{Q^{2}}{16 \pi \varepsilon_{0} \varepsilon_{r}}\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$
B.$W_{e}=\frac{Q^{2}}{8 \pi \varepsilon_{0} \varepsilon_{r}}\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$
C.$W_{e}=\frac{Q^{2}}{8 \pi \varepsilon_{0} \varepsilon_{r}} \ln \frac{R_{2}}{R_{1}}$
D.$W_{e}=\frac{Q^{2}}{32 \pi \varepsilon_{0} \varepsilon_{r}}\left(R_{1}-R_{2}\right)$
|
B
|
|
一根无限长细导线载有电流 $I$ ,折成图6-1所示的形状,圆弧部分的半径为 $R$ ,则圆心处磁感应强度 $B$ 的大小为 。
A.$\frac{\mu_{0} I}{4 \pi R}+\frac{3 \mu_{0} I}{8 R}$
B.$\frac{\mu_{0} I}{2 \pi R}+\frac{3 \mu_{0} I}{8 \pi R}$
C.$\frac{\mu_{0} I}{4 \pi R}-\frac{3 \mu_{0} I}{8 R}$
D.$\frac{\mu_{0} I}{4 R}+\frac{\mu_{0} I}{2 \pi R}$
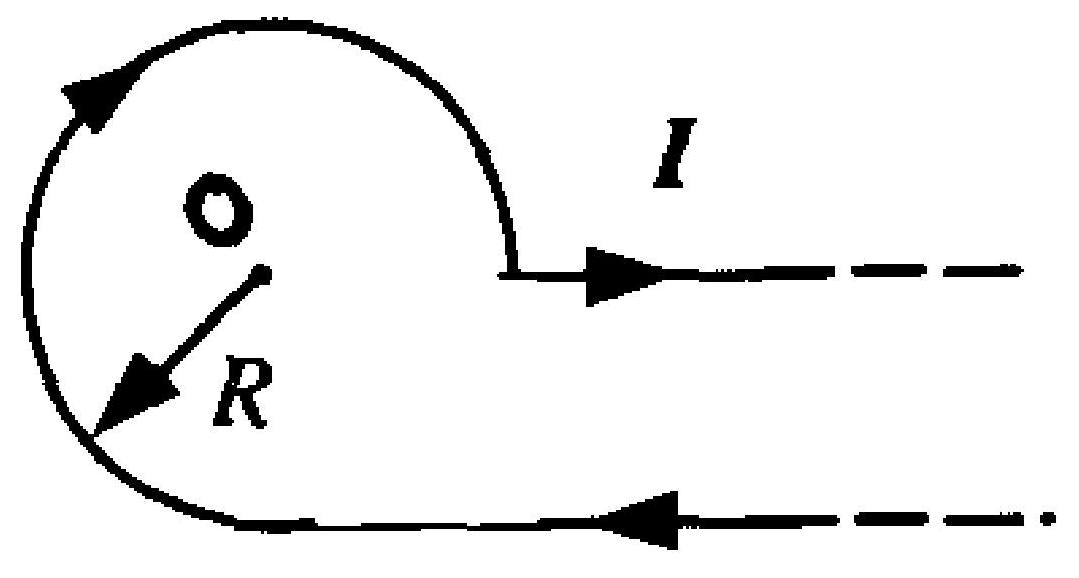
图6-1
|
B
|
|
如图6-2所示,圆形回路 $L$ 和圆电流 $I$ 同心共面,则磁场强度沿 $L$ 的环流为 。
A.$\oint_{L} \boldsymbol{H} \cdot \mathrm{~d} \boldsymbol{l}=0$ ,因为 $L$ 上 $\boldsymbol{H}$ 处处为零
B.$\oint_{L} \boldsymbol{H} \cdot \mathrm{~d} \boldsymbol{l}=0$ ,因为 $L$ 上 $\boldsymbol{H}$ 处处与 $\mathrm{d} \boldsymbol{l}$垂直
C.$\oint_{L} \boldsymbol{H} \cdot \mathrm{~d} \boldsymbol{l}=I$ ,因为 $L$ 包围电流 $I$
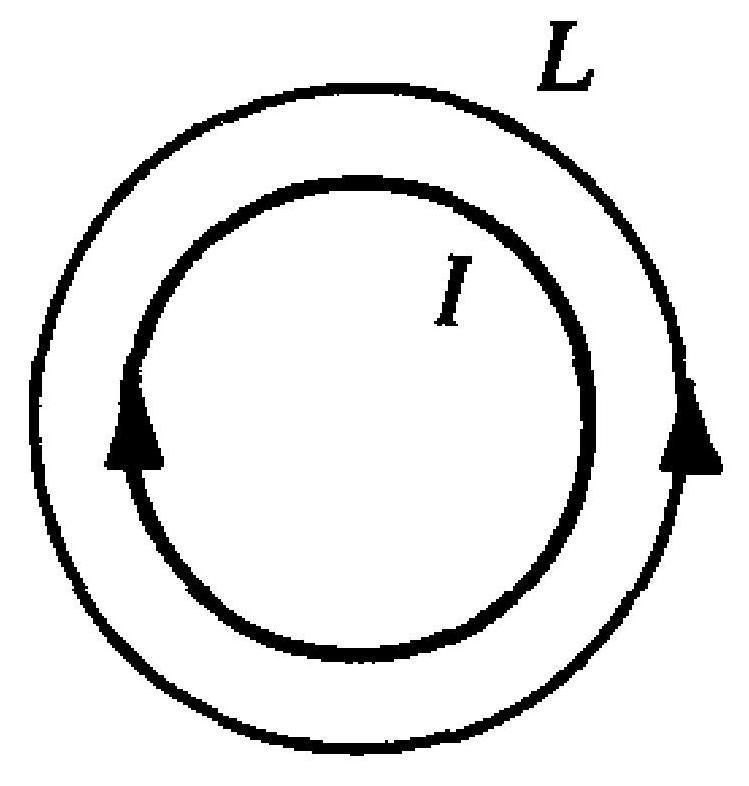
图6-2
D.$\oint_{L} \boldsymbol{H} \cdot \mathrm{~d} \boldsymbol{l}=-I$ ,因为 $L$ 包围电流 $I$ 且绕
向与 $I$ 相反
|
C
|
|
对于安培环路定理的理解,正确的是:(所讨论的空间处在稳恒磁场中 。
A.若 $\oint_{\boldsymbol{L}} \boldsymbol{H} \cdot \mathrm{d} \boldsymbol{l}=0$ ,则在回路 $L$ 上必定是 $\boldsymbol{H}$ 处处为零
B.若 $\oint_{L} \boldsymbol{H} \cdot \mathrm{~d} \boldsymbol{l}=0$ ,则回路 $L$ 必定不包围电流
C.若 $\oint_{L} \boldsymbol{H} \cdot \mathrm{~d} \boldsymbol{l}=0$ ,则回路 $L$ 所包围传导电流的代数和为零
D.回路 $L$ 上各点的 $\boldsymbol{H}$ 仅与回路 $L$ 包围的电流有关
|
C
|
|
一无限长薄圆筒形导体上均匀分布着电流,圆筒半径为 $R$ ,厚度可忽略不计,如图6- 3 所示。在下面的四个图中,$r$ 轴表示沿垂直于薄圆筒轴线的径向,坐标原点与圆筒轴线重合,则这四个图中哪一条曲线正确地表示出了载流
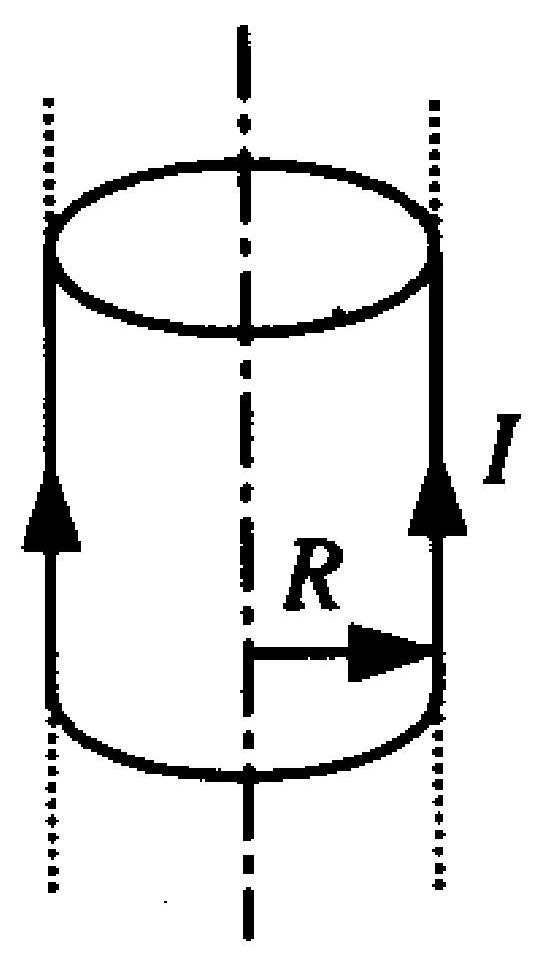
图 6-3
薄圆筒在空间的磁场分布 。
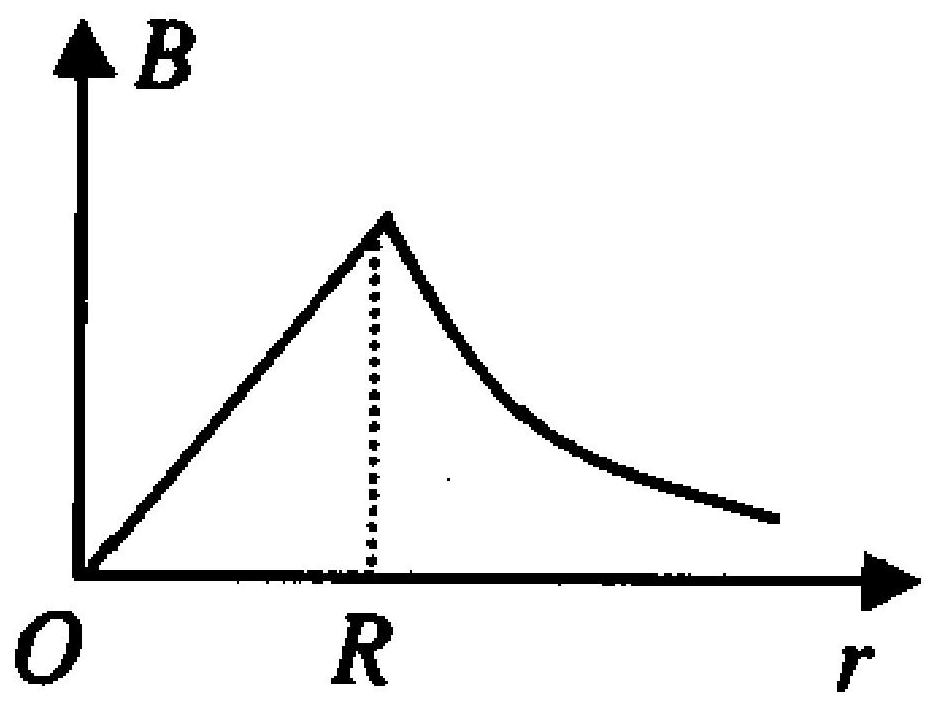
A.
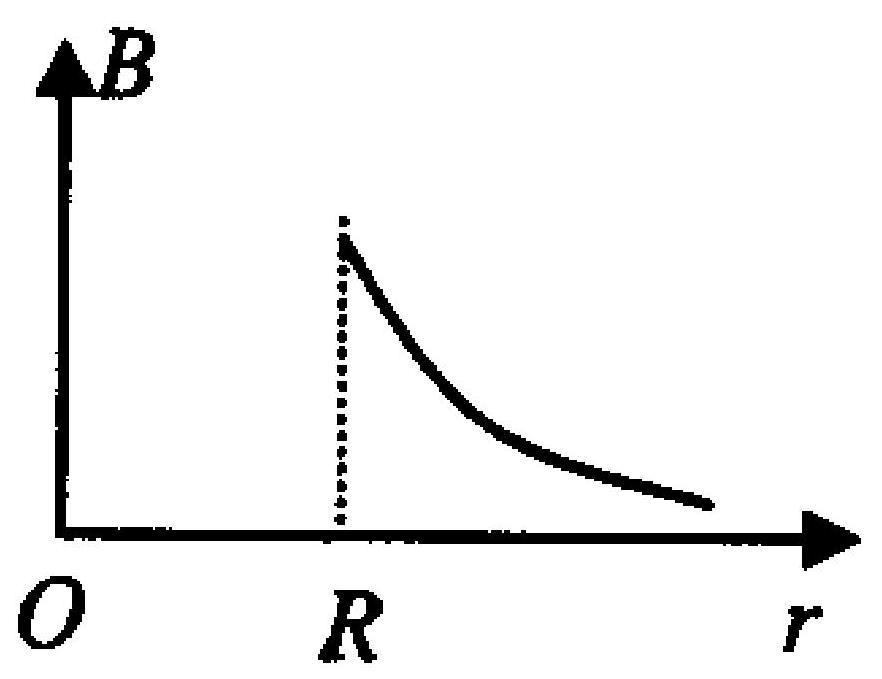
B.
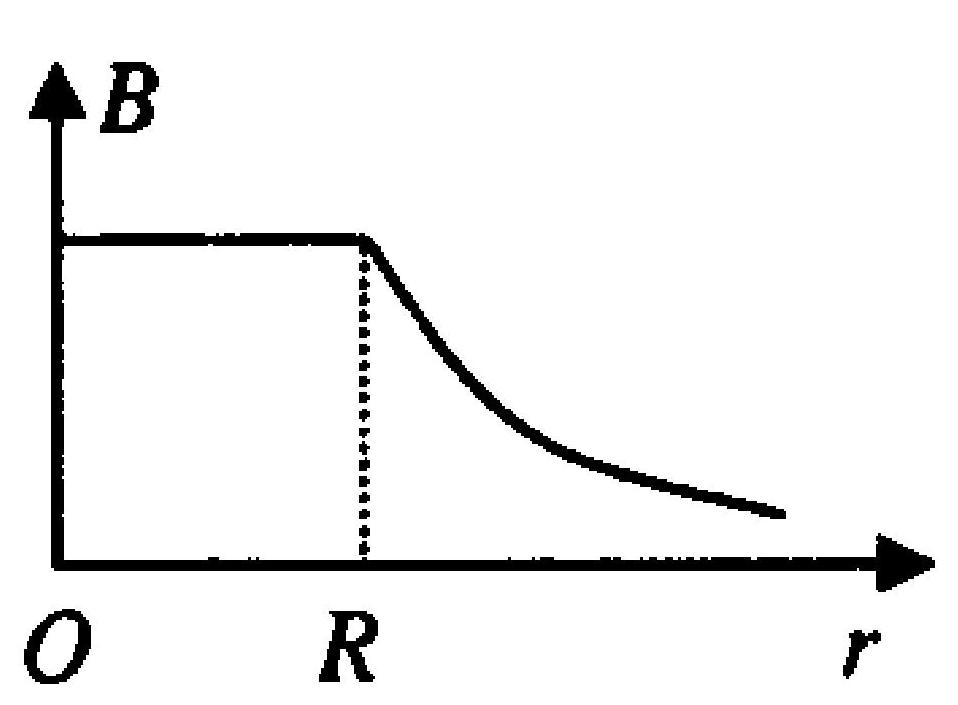
C.
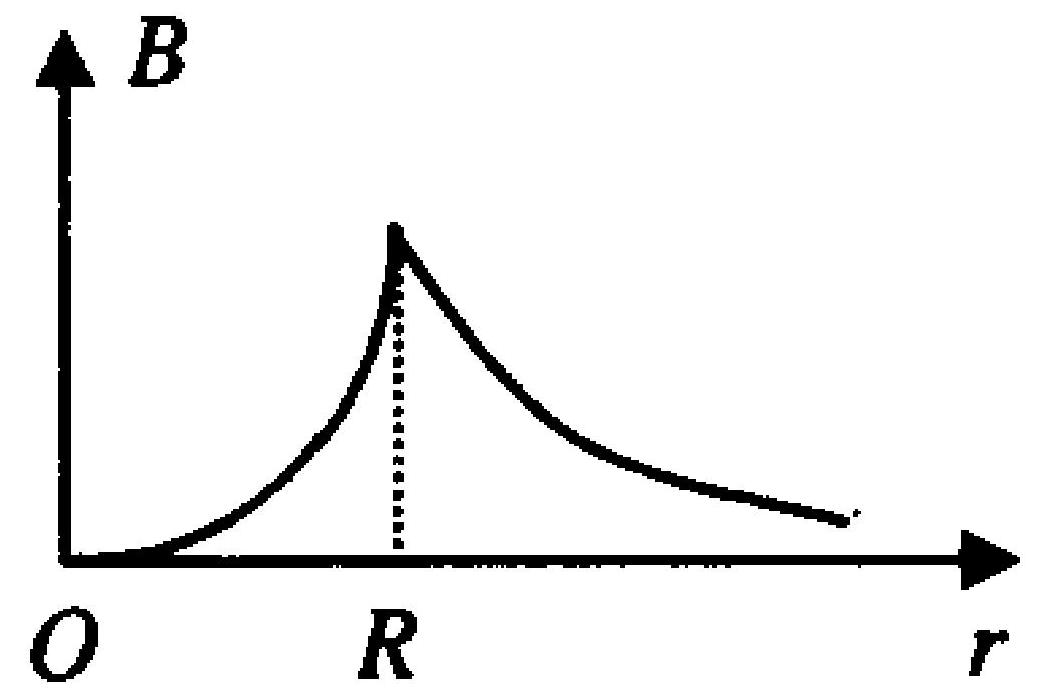
D.
|
B
|
|
如图6-4所示,将一均匀分布着电流的无限大载流平面放入均匀磁场中,电流方向与该磁场垂直。现已知载流平面两侧的磁感应强度分别为 $B_{1}$ 和 $B_{2}$ ,则该载流平面上的电流密度 $j$ 为
A.$\frac{B_{2}-B_{1}}{2 \mu_{0}}$
B.$\frac{B_{2}-B_{1}}{\mu_{0}}$
C.$\frac{B_{1}+B_{2}}{2 \mu_{0}}$
D.$\frac{B_{1}+B_{2}}{\mu_{0}}$
|
C
|
|
一根半径为 $R$ 的无限长直铜导线,载有电流 $I$ ,电流均匀分布在导线的横截面上。在导线内部通过中心轴作一横切面 $S$(如图6-5所示),则通过横切面 $S$ 上每单位长度的磁通量 $\Phi_{m}$ 为 。
A.$\frac{\mu_{0} I}{4 \pi R}$
B.$\frac{\mu_{0} I}{4 \pi}$
C.$\frac{\mu_{0} I}{2 \pi}$
D.$\frac{\mu_{0} I}{2 \pi R^{2}}$
|
C
|
|
一线圈载有电流 $I$ ,处在均匀磁场 $\boldsymbol{B}$ 中,线圈形状及磁场方向如图6-6所示,线圈受到磁力矩的
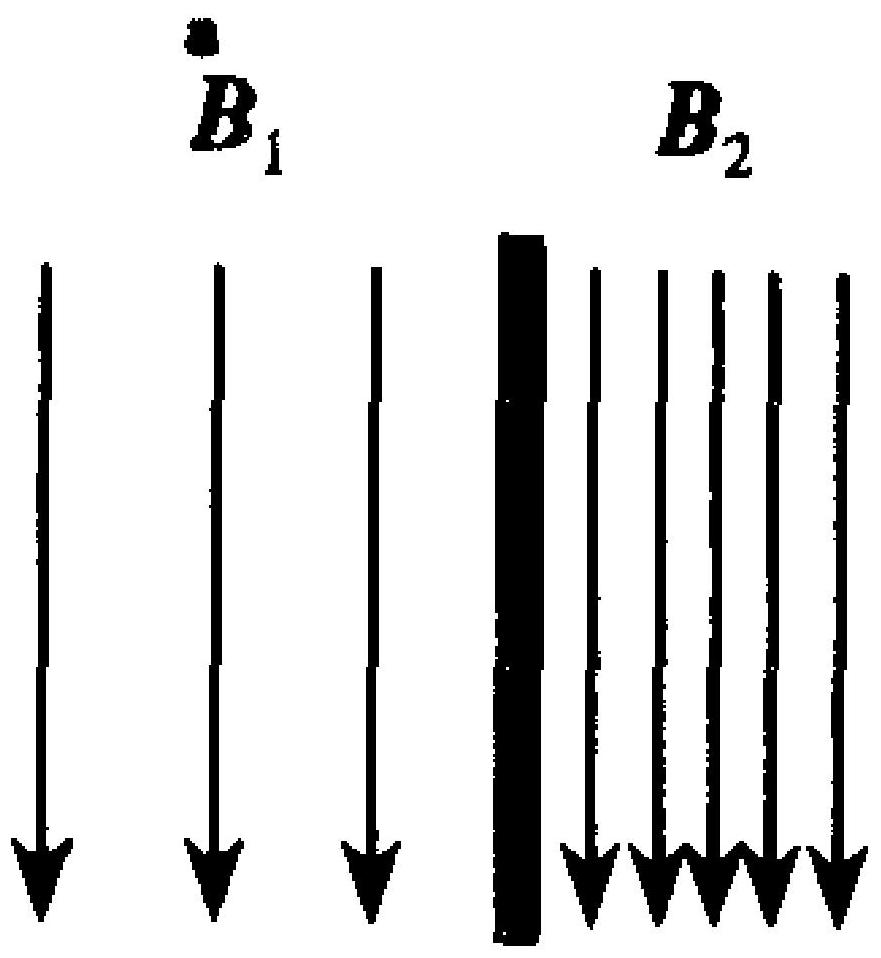
图 6-4
大小和转动情况为(转动方向以从 $\mathrm{O}_{1}$ 看向 $\mathrm{O}_{1}^{\prime}$ 或从 $\mathrm{O}_{2}$ 看向 $\mathrm{O}_{2}^{\prime}$ 为准) 。
A.$M_{m}=\frac{5}{2} \pi R^{2} I B$ ,绕 $\mathrm{O}_{1} \mathrm{O}_{1}^{\prime}$
轴逆时针转动轴顺时针转动
C.$M_{m}=\frac{3}{2} \pi R^{2} I B$ ,绕 $\mathrm{O}_{2} \mathrm{O}_{2}^{\prime}$
图 6-6
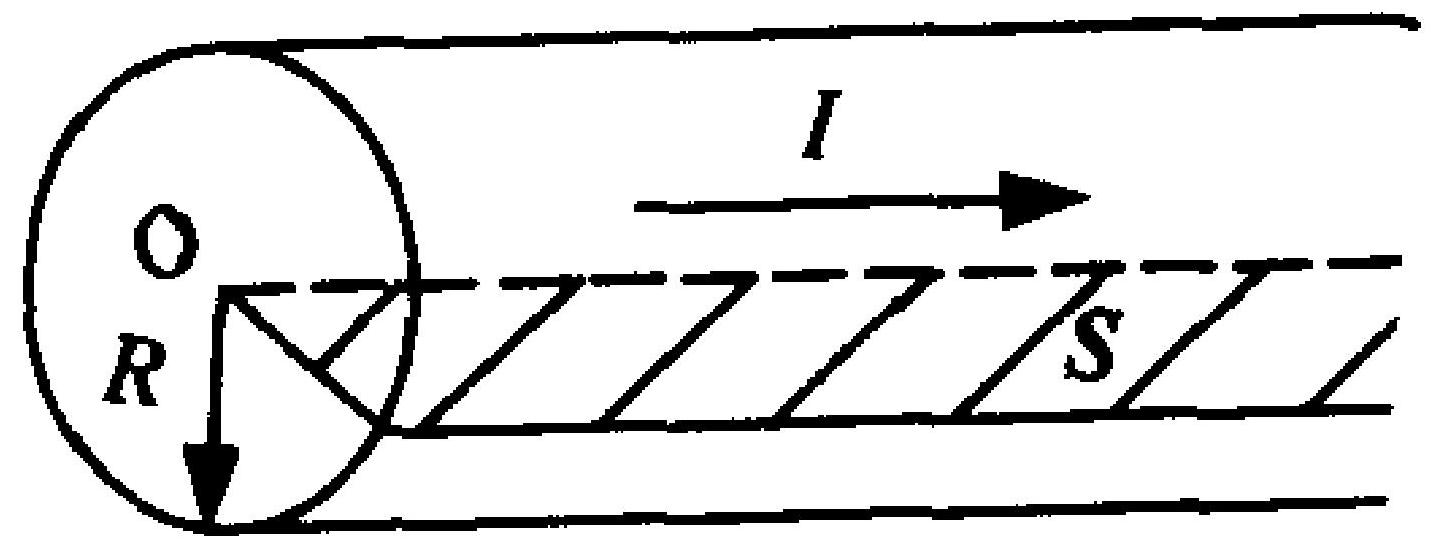
图6-5
准)()。 (
A.$M_{m}=\frac{5}{2} \pi R^{2} I B$, 绕 $\mathrm{O}_{1} \mathrm{O}_{1}^{\prime}$
轴逆时针转动
B.$M_{m}=\frac{5}{2} \pi R^{2} I B$ ,绕 $\mathrm{O}_{1} \mathrm{O}_{1}^{\prime}$
轴顺时针转动
时针转动
轴顺时针转动
D.$M_{m}=\frac{3}{2} \pi R^{2} I B$ ,绕 $\mathrm{O}_{2} \mathrm{O}_{2}^{\prime}$ 轴逆时针转动
|
A
|
|
如图6-7所示,通有电流 $I$ 的金属薄片,置于垂直于薄片的均匀磁场 $B$ 中,则金属片上 $\mathrm{a}, \mathrm{b}$ 两端点的电势相比为()。
A.$U_{\mathrm{a}}>U_{\mathrm{b}}$
B.$U_{\mathrm{a}}=U_{\mathrm{b}}$
C.$U_{\mathrm{a}}<U_{\mathrm{b}}$
D.无法确定。
|
D
|
|
如图6-8所示,均匀磁场的磁感应强度为 $\boldsymbol{B}$ ,方向沿 $\boldsymbol{y}$ 轴正向,欲要使电量为 $q$ 的正离子沿 $x$ 轴正向作匀速直线运动,则必须加一个均匀电场 $\boldsymbol{E}$ ,其大小和方向为( )。
A.$E=\frac{B}{v}, \quad E$ 沿 $z$ 轴正向
B.$E=\frac{B}{v}, E$ 沿 $y$ 轴正向
C.$E=B v, \quad E$ 沿 $z$ 轴正向
D.$E=B v, E$ 沿 $z$ 轴负向

图 6-7
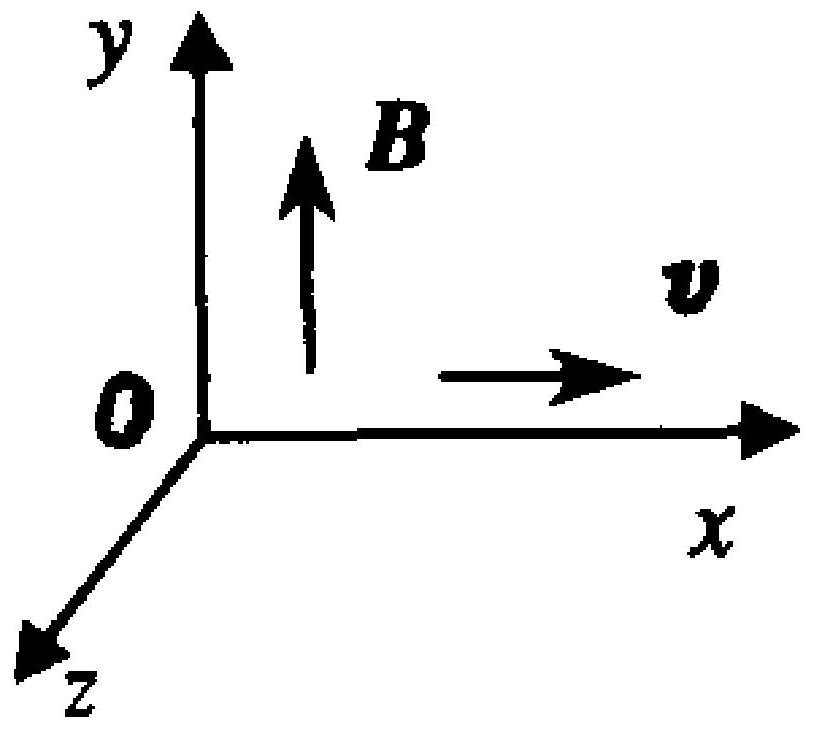
图6-8
|
B
|
|
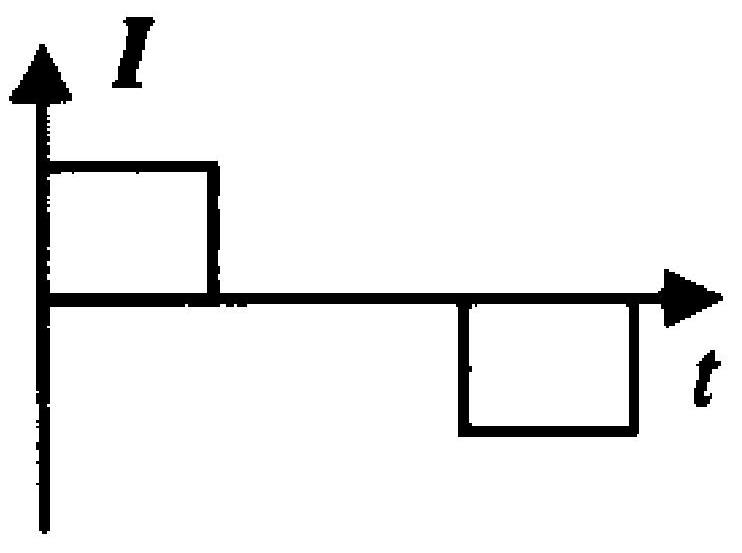
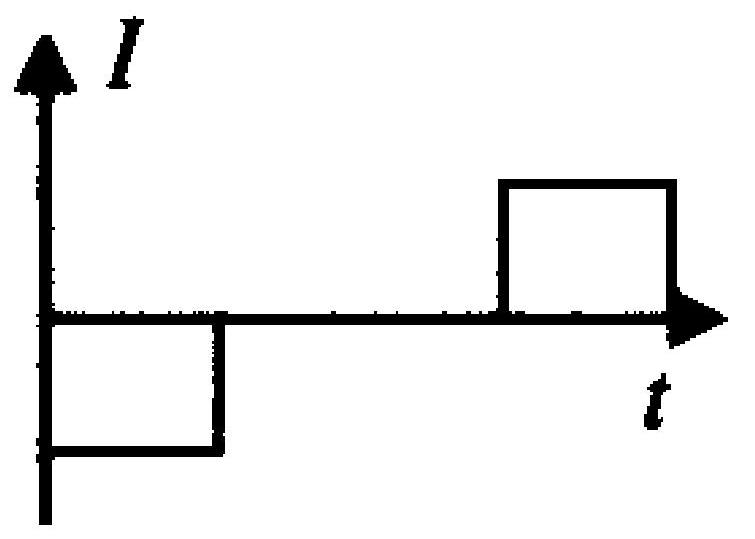
如图 7-1 所示,一矩形导体框,以速度 $\nu$ 从 a 处进入一均匀磁场区域并从 b 处出来。若不计导体框的自感,下面哪条曲线正
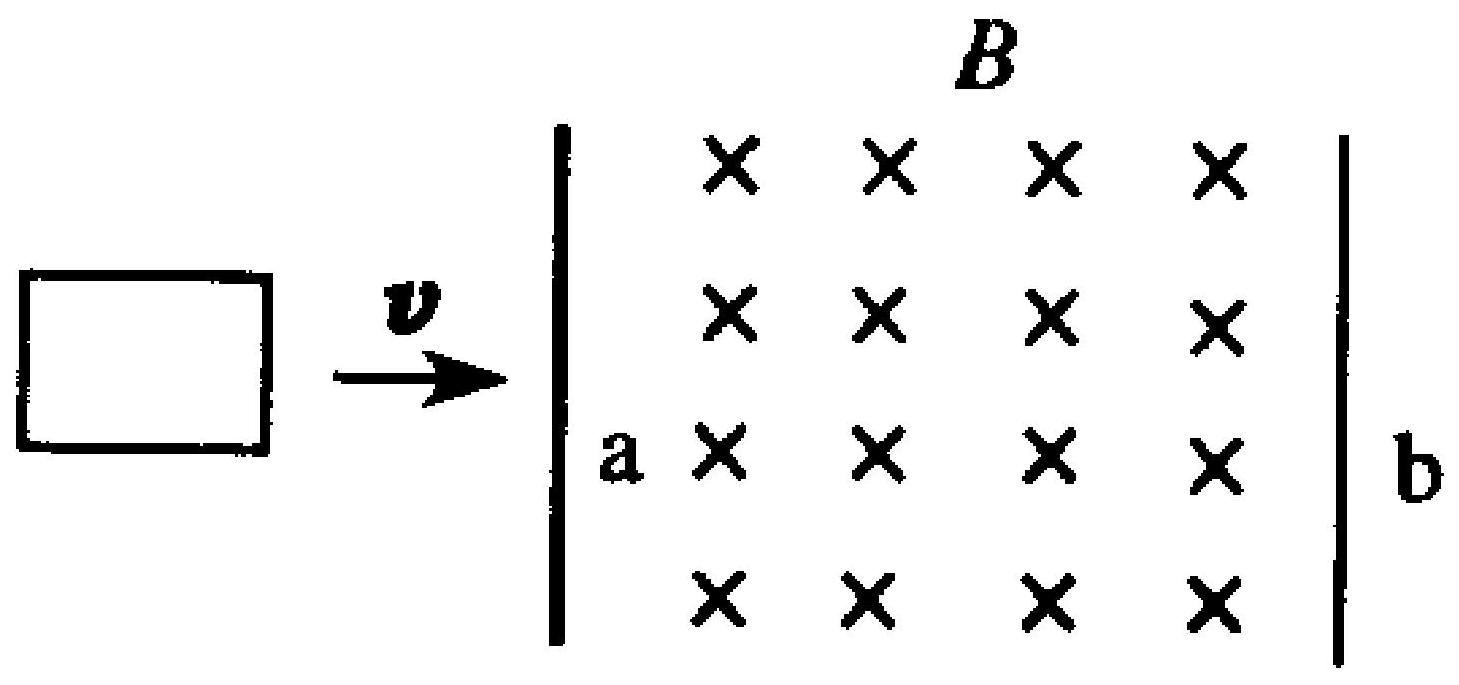
图 7-1
确地表示了线圈中的感应电流随时间的变化关系(以顺时针方向为正)

A
B
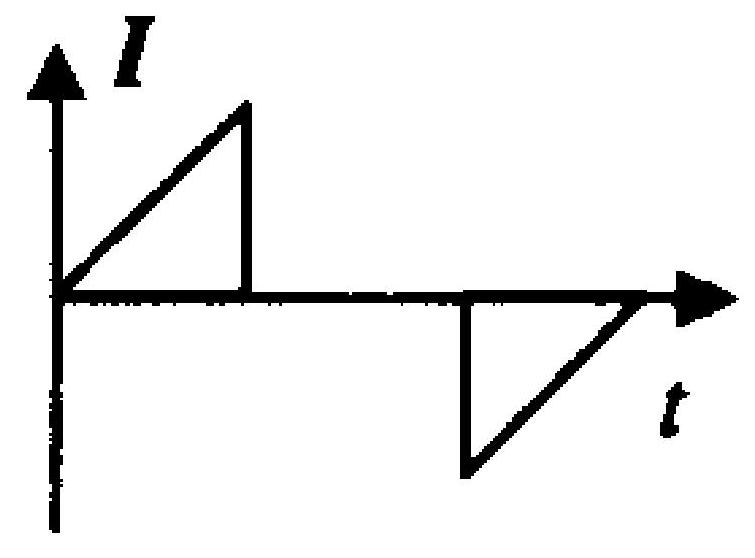
C
D
|
B
|
|
将一根导线弯折成半径为 $R$ 的 $3 / 4$ 圆弧 abcd ,置于均匀磁场 $B$ 中,$B$ 垂直于导线平面,如图7-2所示。当导线沿角 $\operatorname{aod}$ 的角平分线方向以速度 $v$ 向右运动时,导线中产生的感应电动势 $\mathscr{E}_{i}$ 为
。
A. 0
B.$v R B$
C.$\sqrt{2} v R B$
D.$\frac{\sqrt{2}}{2} v R B$

图7-2
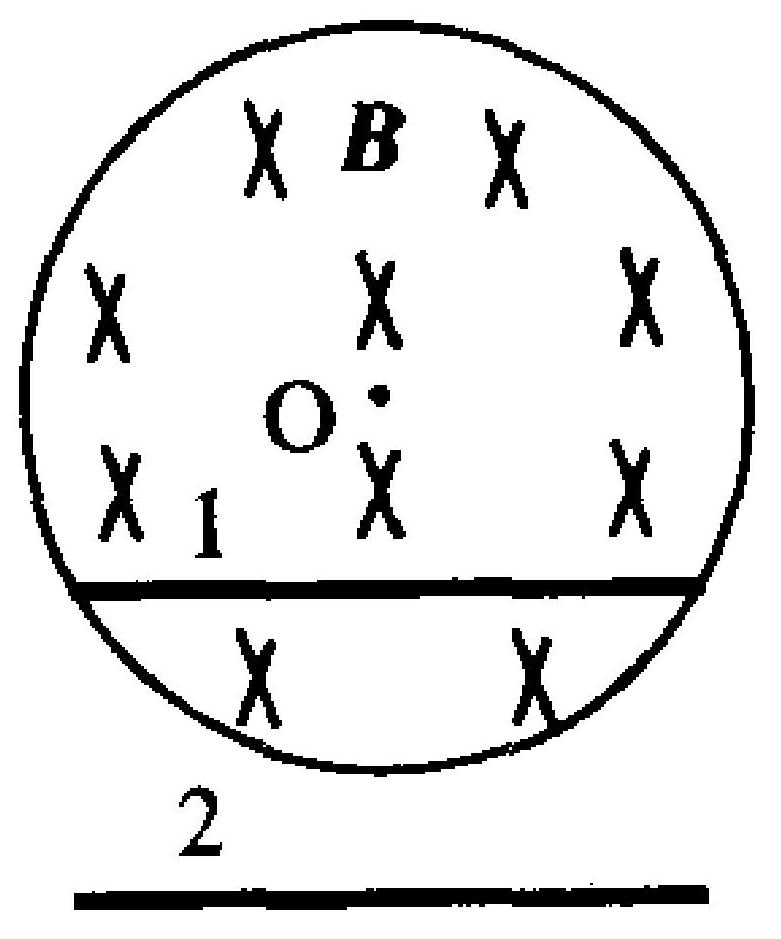
图 7-3
|
C
|
|
在圆柱形空间内有一均匀磁场区,如图7-3所示,在磁场内外各放有一长度相同的金属棒(在图中位置 1,2 处),当磁场 $\boldsymbol{B}$的大小以速率 $\frac{\mathrm{d} B}{\mathrm{~d} t}$ 均匀变化时,下列说法正确的是( )。
A. 1 处的棒相对磁场静止,故 $\mathscr{E}_{1}=0$
B. 1 处的棒处在变化的磁场中,故 $\mathscr{E}_{1}=0$
C. 2 处的棒处在磁场以外的空间,故 $\mathscr{E}_{2}=0$
D. 2 处的棒虽处在 $\boldsymbol{B}=0$ 的空间,但 $\boldsymbol{E}_{\text {涡 }} \neq 0$ 。故 $\mathscr{E}_{2} \neq 0$
|
C
|
|
一个电阻为 $R$ ,自感系数为 $L$ 的线圈,将它接在一个电动势为 $\mathscr{E}(t)$ 的交变电源上,线圈的自感电动势 $\mathscr{E}_{L}=-L \frac{\mathrm{~d} I}{\mathrm{~d} t}$ ,则流过线圈的电流为()。
A.$\frac{\mathscr{E}(t)}{R}$
B.$\frac{\mathscr{E}_{L}}{R}$
C.$\frac{\mathscr{E}(t)+\mathscr{E}_{L}}{R}$
D.$\frac{\mathscr{E}(t)-\mathscr{E}_{L}}{R}$
|
B
|
|
下列说法中正确的是()。
A.按照线圈自感系数的定义式 $L=\Phi / I, I$ 越小,$L$ 就越大
B.自感是对线圈而言的,对一个无线圈的导线回路是不存在自感的
C.位移电源只在平行板电容器中存在
D.位移电流的本质也是电荷的定向运动,当然也能激发磁场
E.以上说法均不正确。
|
C
|
|
两个相距不太远的平面圆线圈,怎样放置可使其互感系数近似为零(设其中一线圈的轴线恰通过另一线圈的圆心) 。
A.两线圈的轴线相互平行
B.两线圈的轴线相互垂直
C.两线圈的磁矩成反平行
D.两线圈无论如何放置,互感系数也不为零
|
C
|
|
已知平行板电容器的电容为 $C$ ,两极板间的电势差 $U^{r}$ 随时间变化,其间的位移电流为 。
A.$C \frac{\mathrm{~d} U}{\mathrm{~d} t}$
B.$\frac{\mathrm{d} D}{\mathrm{~d} t}$
C.$C U$
D. 0
|
A
|
|
在以下矢量场中,属保守力场的是 。
A.静电场
B.涡流电场
C.稳恒磁场
D.变化磁场
|
D
|
|
两个体积不等的容器,分别储有氦气和氧气,若它们的压强相同,温度相同,则下列各量中相同的是()。
A.单位体积中的分子数
B.单位体积中的气体内能
C.单位体积中的气体质量
D.容器中的分子总数
|
B
|
|
两个体积相等的容器中,分别储有氦气和氢气,以 $E_{1}$ 和 $E_{2}$分别表示氦气和氢气的内能,若它们的压强相同,则()。
A.$E_{1}=E_{2}$ 。
B.$E_{1}>E_{2}$
C.$E_{1}<E_{2}$ 。
D.无法确定
|
C
|
|
两个容器中分别装有氮气和二氧化碳,它们的温度相同,则下列各量中相同的是()。
A.分子平均动能。
B.分子平均速率
C.分子平均平动动能。
D.最概然速率
|
C
|
|
4 mol 的多原子分子理想气体,当温度为 $T$ 时,其内能为 ( )。
A. $12 k T$
B. $10 k T$
C. $12 R T$
D. $10 R T$
|
B
|
|
当气体的温度升高时,麦克斯韦速率分布曲线的变化为 ( )。
A.曲线下的面积增大,最概然速率增大
B.曲线下的面积增大,最概然速率减小
C.曲线下的面积不变,最概然速率增大
D.曲线下的面积不变,最概然速率减小
E.曲线下的面积不变,曲线的最高点降低
|
C
|
|
下列对最概然速率 $v_{P}$ 的表述中,正确的是()。
A.$v_{P}$ 是气体分子可能具有的最大速率
B.分子速率取 $v_{P}$ 的概率最大
C.速率分布函数 $f(v)$ 取极大值时所对应的速率就是 $v_{P}$
D.就单位速率区间而言,分子速率处于 $v_{P}$ 附近的概率最大
|
C
|
|
$f(v)$ 为速率分布函数,则速率 $v<v_{p}$ 的分子平均速率表达式为( )。
A. $\bar{v}=\int_{0}^{v_{P}} f(v) \mathrm{d} v$
B. $\bar{v}=\frac{\int_{0}^{v_{p}} v f(v) d v}{\int_{0}^{v_{p}} f(v) d v}$
C. $\bar{v}=\int_{0}^{v_{P}} v f(v) \mathrm{d} v$
D. $\bar{v}=\frac{1}{2} v$
|
A
|
|
体积固定的容器中,有一定量的理想气体,当温度逐渐升高时(设分子有效直径保持不变),分子的平均碰撞次数 $\bar{Z}$ 和平均自由程 $\bar{\lambda}$ 的变化为()。
A. $\bar{Z}$ 增大,त增大
B. $\bar{Z}$ 增大, $\bar{\lambda}$ 不变
C. $\bar{Z}$ 增大,त减少
D. $\bar{Z}$ 和 $\bar{\lambda}$ 都保持不变
|
D
|
|
下列表述中错误的为()。
A.系统由外界吸热时,内能必然增加,温度升高
B.考虑到热量 $Q$ 和功 $A$ 都是过程量,因此,对于任何变化过程,系统所吸收的热量和外界对系统做功的总和,不仅与系统始、末状态有关,而且与具体过程有关
C.在等体过程中,系统内能的变化为 $\Delta E=\frac{M}{\mu} C_{V}\left(T_{2}-T_{1}\right)$ ,而在等压过程中系统内能变化为 $\Delta E=\frac{M}{\mu} C_{P}\left(T_{2}-T_{1}\right)$
D.热机效率的一般表达式为 $\eta=1-\frac{Q_{2}}{Q_{1}}=1-\frac{T_{2}}{T_{1}}$
|
B
|
|
如图9-1所示,理想气体卡诺循环过程中两条绝热线下面的面积为 $S_{1}$和 $S_{2}$ ,则( )。
A.$S_{1}>S_{2}$
B.$S_{1}=S_{2}$
C.$S_{1}<S_{2}$
D.无法确定
|
C
|
|
某理想气体分别进行了如图9-2所示的两个卡诺循环( $a b c d a$ )I 和 $\mathbb{I}\left(a^{\prime} b^{\prime} c^{\prime} d^{\prime} a^{\prime}\right)$ ,已知两低温热源温度相
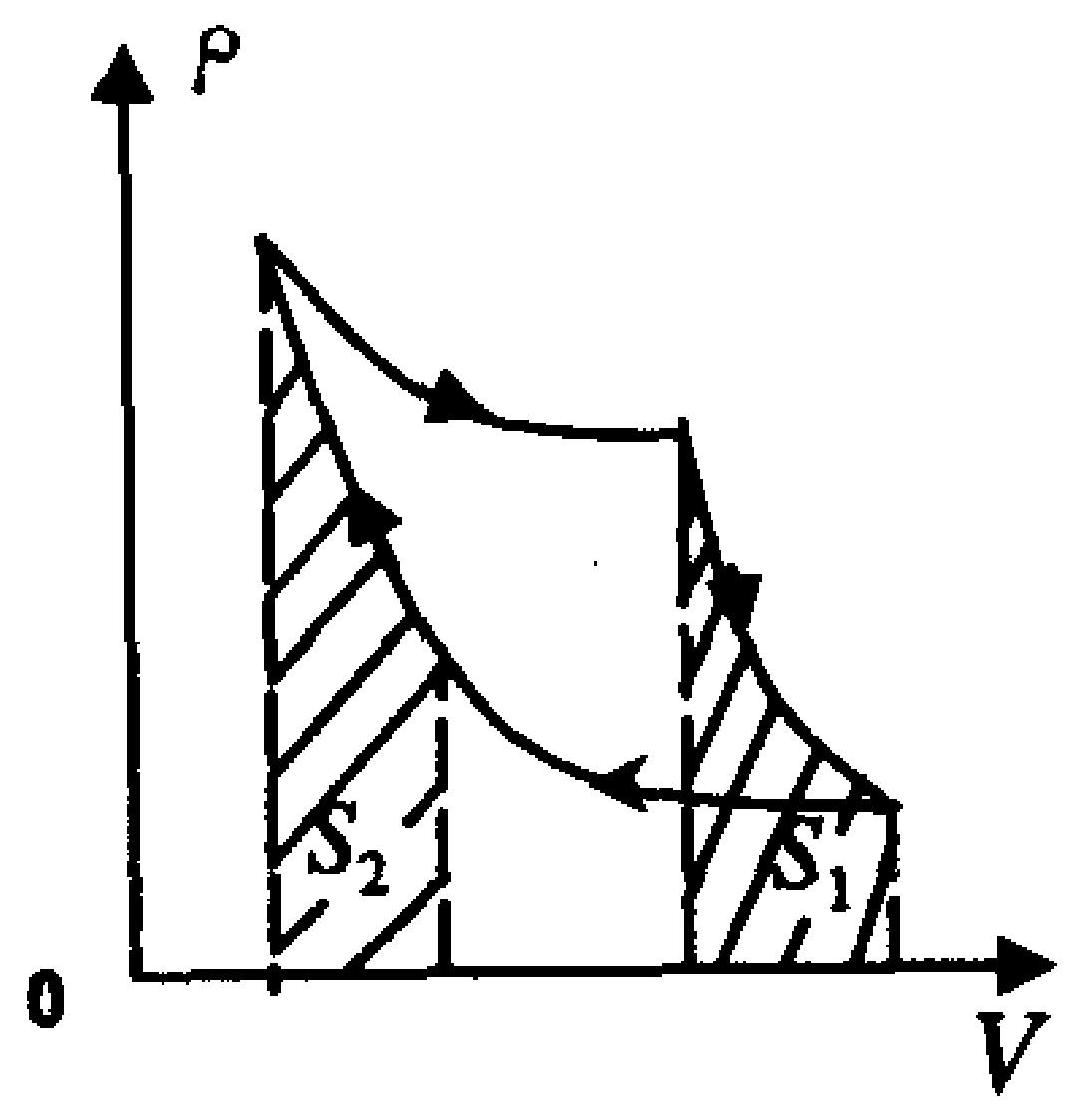
图 9-1
A.$\eta<\eta^{\prime}, Q<Q^{\prime}$
B.$\eta>\eta^{\prime}, Q<Q^{\prime}$
C.$\eta<\eta^{\prime}, Q>Q^{\prime}$
D.$\eta>\eta^{\prime}, Q>Q^{\prime}$
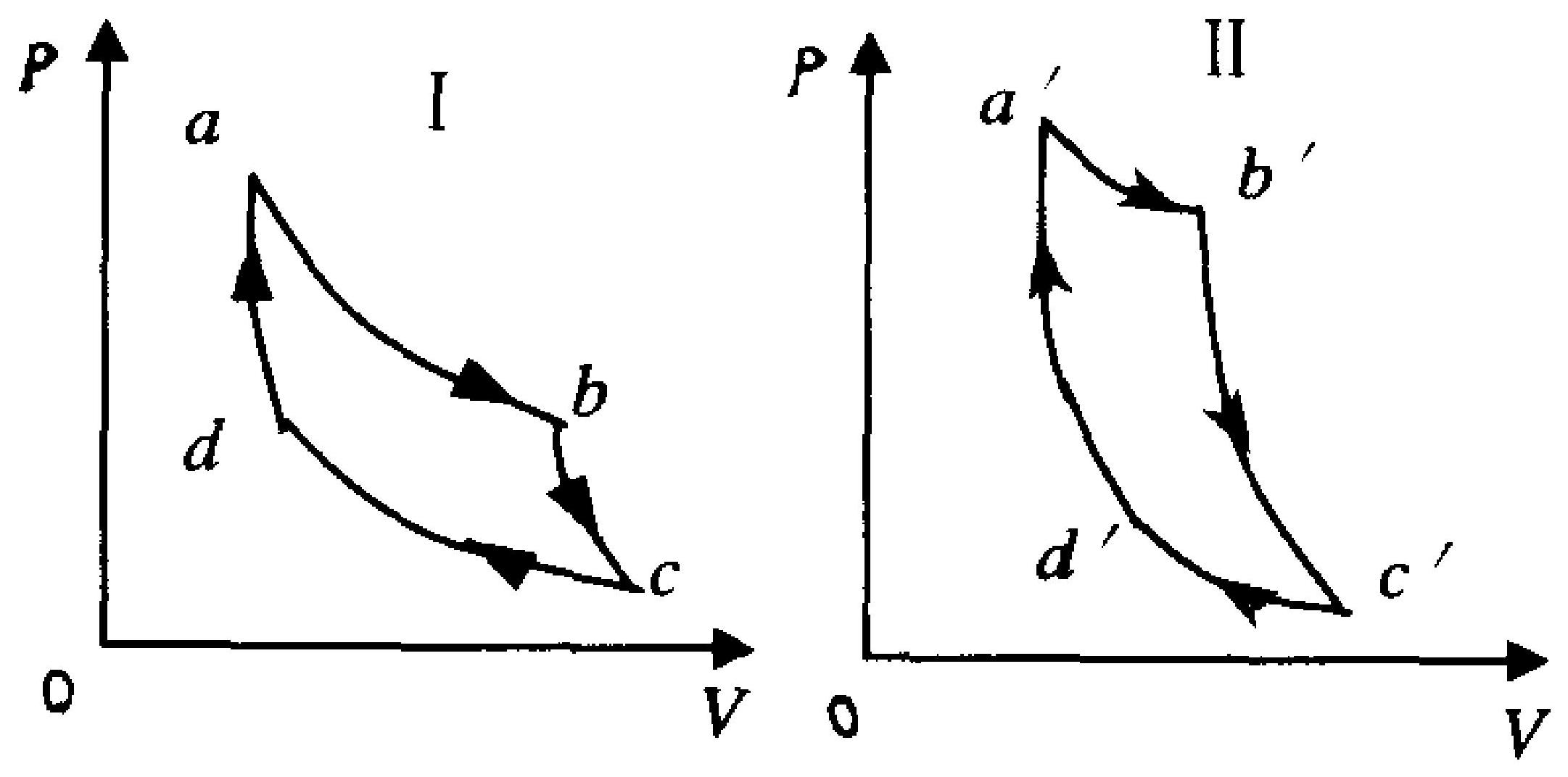
图9-2
|
C
|
|
某理想气体状态变化时,内能随压强的变化关系如图9-3中的直线 $a b$ 所示,则 $a$ 到 $b$ 的变化过程一定是 。
A.等压过程
B.等体过程
C.等温过程
D.绝热过程
|
B
|
|
若高温热源的温度为低温热源温度的 $n$ 倍,以理想气体为工作物质的卡诺
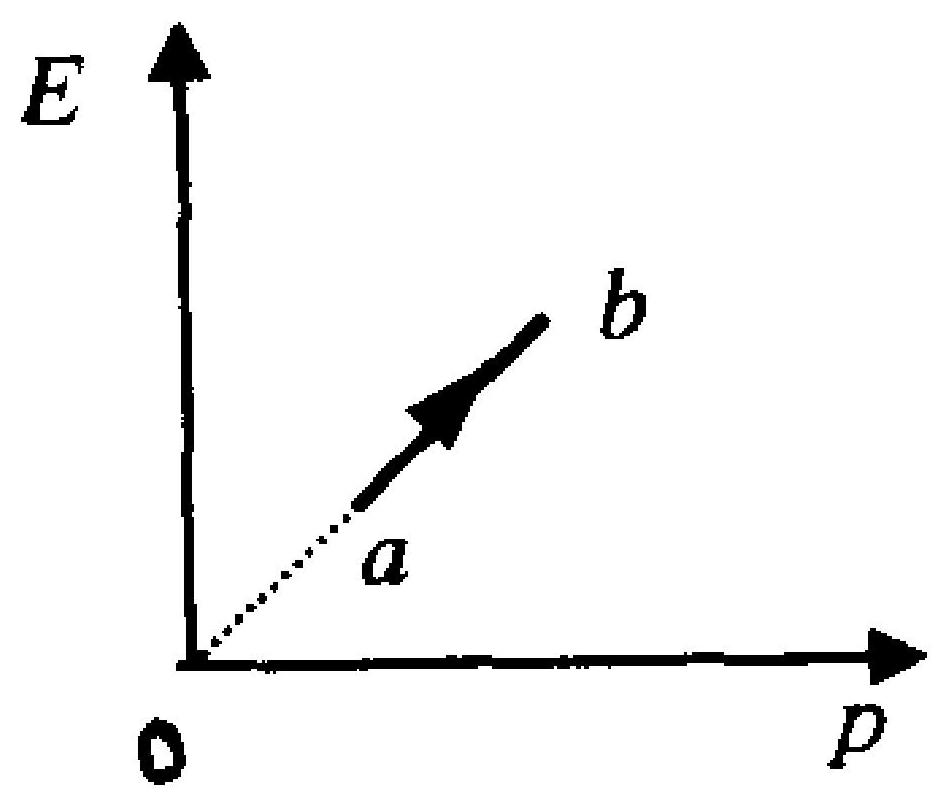
图 9-3
A.$\frac{n+1}{n}$
B.$\frac{n-1}{n}$
C.$n$
D.$n-1$
|
C
|
|
分子总数相同的三种理想气体 $\mathrm{He}, \mathrm{O}_{2}$ 和 $\mathrm{CO}_{2}$ ,它们各自独立地进行等压膨胀,对外做功 $A$ 与系统内能量 $\Delta E$ 的比值最小的气体是 。
A. He
B. $\mathrm{O}_{2}$
C. $\mathrm{CO}_{2}$
D.无法确定
|
C
|
|
按上题,若三种气体从同一初态出发,各自独立地进行等压膨胀,且吸收的热量相等,则终态的体积最大的气体是 。
A. He
B. O 2
C. $\mathrm{CO}_{2}$
D.三种气体终态的体积相同
|
A
|
|
热力学第二定律指出了热力学过程进行的方向性和条件,下列表述中正确的是()。
A.功可以全部转化为热量,但热量不能全部转化为功
B.热量可以从高温物体传到低温物体,但不能从低温物体传到高温物体
C.对孤立系统来讲,自发过程总是按系统嫡值增加的方向进行
D.对孤立系统来讲,其内部发生的过程,总是由概率小的宏观态向概率大的宏观态进行
E.不可逆过程就是不能向相反方向进行的过程
F.一切自发过程都是不可逆的
|
D
|
|
弹簧振子的振幅增加 1 倍,则 。
A.振动周期增加 1 倍
B.最大速度增加 1 倍
C.总能量增加 2 倍
D.最大加速度不变
|
B
|
|
质点作简谐振动,其速度与时间的曲线如图10-1所示,则该质点的振动方程中的初相位应为
)。
A.$\frac{\pi}{6}$
B.$\frac{5 \pi}{6}$
C.$-\frac{\pi}{6}$
D.$-\frac{5 \pi}{6}$
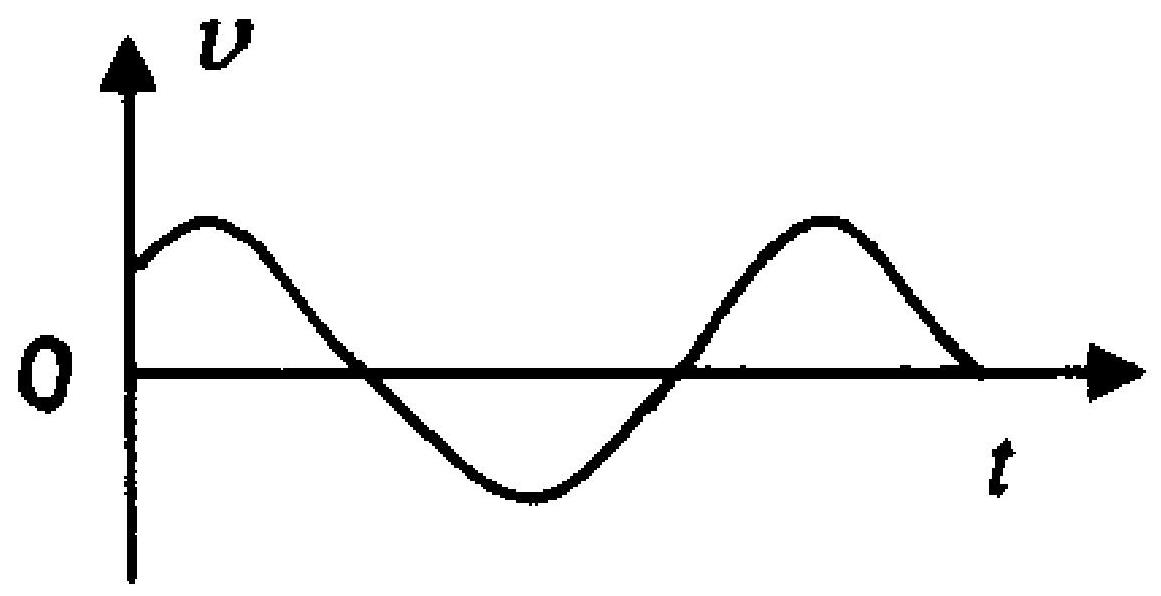
图10-1
|
C
|
|
下列说法中正确的是()。
A.同方向,同频率的两个简谐振动合成后,合振动仍为简谐振动
B.同方向,不同频率的两个简谐振动合成后,合振动不是简谐振动
C.同频率,相互垂直的两个简谐振动合成后,一般情况下是椭圆运动
D.不同频率,相互垂直的两个简谐振动合成后,合振动也可能是简谐振动
|
C
|
|
下列各式是简谐振动的是(其中 $A, B, \omega$ 均为常数)()。
A.$x=A \cos \omega t+B \sin \omega t$
B.$x=A \cos \omega t+B \sin 2 \omega t$
C.$x=A \cos \omega t+2 B \sin \omega t$
D.$x=A \cos \omega t+B$
|
B
|
|
两个振动方向,振幅 $A$ ,频率均相同的简谐振动,每当它们经过振幅一半处时相遇,且运动方向相反,则()。
A.相位差 $\Delta \varphi=\pi$ ,合振幅 $A^{\prime}=0$
B.相位差 $\Delta \varphi=0$ ,合振幅 $A^{\prime}=2 A$
C.相位差 $\Delta \varphi=\frac{2}{3} \pi$ ,合振幅 $A^{\prime}=A$
D.相位差 $\Delta \varphi=\frac{\pi}{2}$ ,合振幅 $A^{\prime}=\sqrt{2} A$
|
C
|
|
质点作简谐振动,其速度最大值为 $V_{m}=3 \times 10^{-2} \mathrm{~m} / \mathrm{s}$ ,振幅 $A=2 \times 10^{-2} \mathrm{~m}$ ,若从速度为正的最大值开始计时,则()。
A.周期 $T=\frac{4}{3}$ ,初相位 $\varphi=0$
B.周期 $T=\frac{4 \pi}{3}$ ,初相位 $\varphi=-\frac{\pi}{2}$
C.最大加速度 $a_{m}=4.5 \times 10^{-2} \mathrm{~m} / \mathrm{s}^{2}$ ,圆频率 $\omega=\frac{3}{2}$
D.周期 $T=4 \pi$ ,初相位 $\varphi=\frac{\pi}{2}$
|
C
|
|
将两个振动方向、振幅、周期均相同的简谐振动合成后,若合振幅和分振动的振幅相同,则这两个分振动的相位差为()。
A.$\frac{\pi}{6}$
B.$\frac{\pi}{3}$
C.$\frac{\pi}{2}$
D.$\frac{2 \pi}{3}$
|
A
|
|
为了测定音叉 $C$ 的振动频率,另选两个和 $C$ 频率相近的音叉 $a$ 和 $b$ ,其频率已知 $v_{a}=500 \mathrm{~Hz}, v_{b}=495 \mathrm{~Hz}$ ,先使音叉 $a$ 和 $c$ 同时振动,测出每秒钟声响加强两次,然后使音叉 $b$ 和 $c$ 同时振动,测出每秒钟声响加强 3 次,则音叉 $c$ 的频率为()。
A. 502 Hz
B. 499 Hz
C. 498 Hz
D. 497 Hz
|
D
|
|
波由一种媒质进入另一种媒质时,其传播速度、频率、波长
"
A.都不发生变化
B.速度和频率变,波长不变
C.都发生变化
D.速度和波长变、频率不变
|
B
|
|
已知 $t=0.5 \mathrm{~s}$ 的波形如图11-1所示,波速大小 $u= 10 \mathrm{~m} / \mathrm{s}$ ,若此时 $P$ 点处媒质元的振动动能在逐渐增大,则波动方程为 。
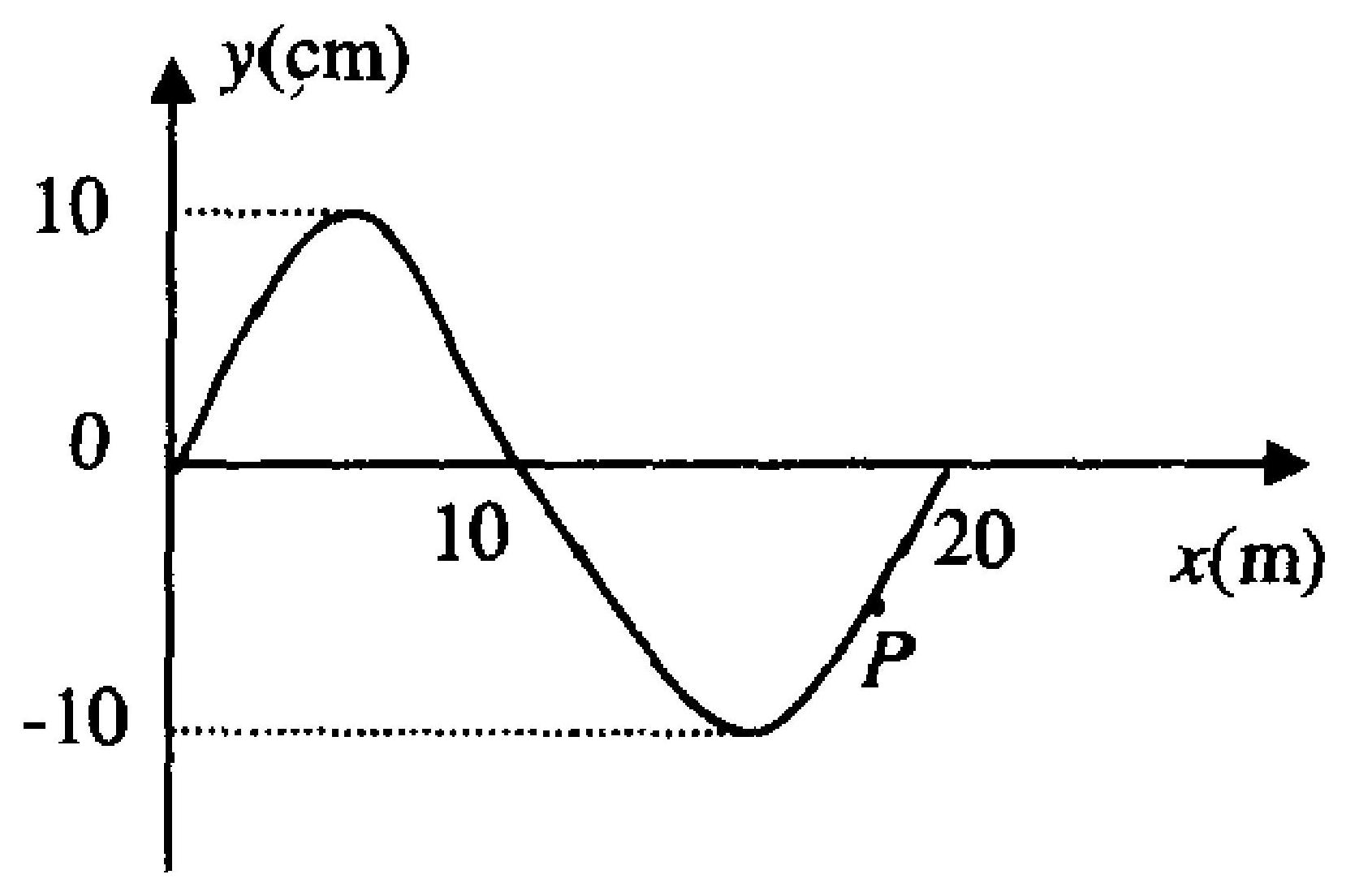
图 11-1
A.$y=10 \cos \left[\pi\left(t+\frac{x}{10}\right)\right](\mathrm{cm})$
B.$y=10 \cos \left[\pi\left(t+\frac{x}{10}\right)+\pi\right](\mathrm{cm})$
C.$y=10 \cos \left[\pi\left(t-\frac{x}{10}\right)\right](\mathrm{cm})$
D.$y=10 \cos \left[\pi\left(t-\frac{x}{10}\right)+\pi\right](\mathrm{cm})$
|
C
|
|
两列波在 $B$ 点相遇,下列说法正确的是()。
A.在某时刻 $t=t_{0}, B$ 点的振幅正好等于两列波振幅之和,则这两列波是相干波
B.两列波是相干波,如果在某一时刻看到 $B$ 点的质元在平衡位置上,则 $B$ 点一定不是干涉加强点
C.两列波是相干波,如果在某时刻看到 $B$ 点的质元距平衡位置为 $y$ ,且 $A_{\min }<y<A_{\max }$ ,那么 $B$ 点一定即不是加强点,也不是减弱点
D.在 $B$ 点,两列波中能流密度大者,振幅必定也大
E.以上说法均不正确
|
C
|
|
图11-2为一平面简谐波在 $t$ 时刻的波形曲线,若此时 $A$ 点处介质质元的振动动能在增大,则()。
A.$A$ 点处质元的弹性势能在减小
B.$B$ 点处质元的振动动能
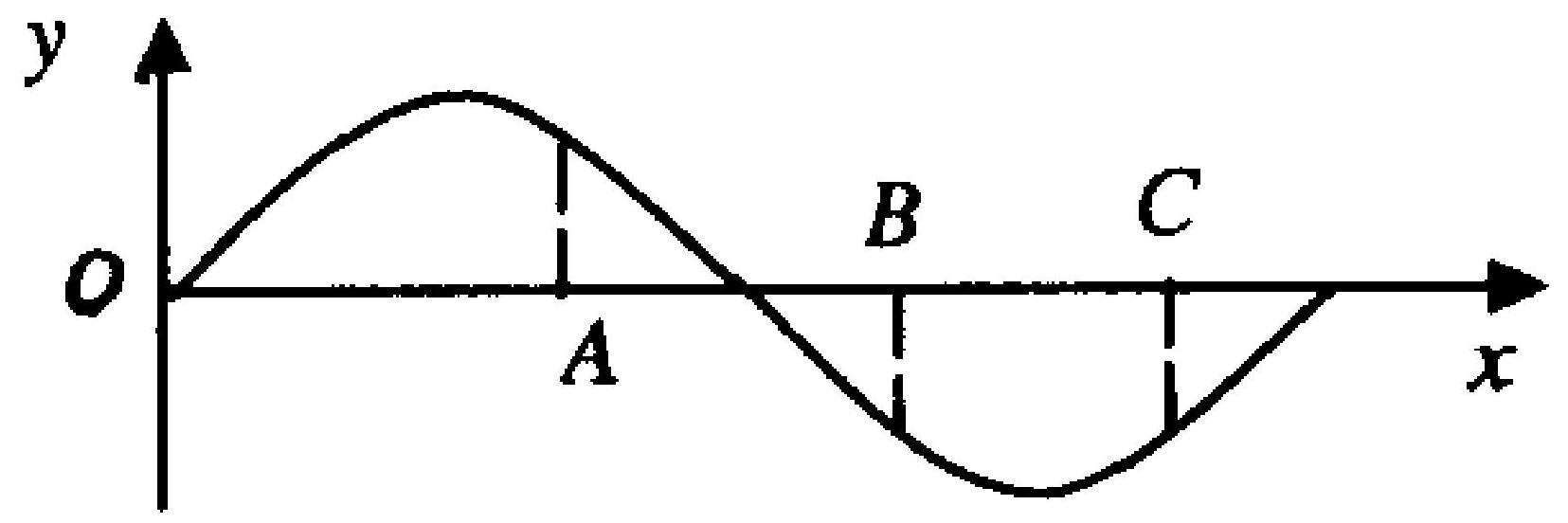
图 11-2
C.波沿 $x$ 轴正方向传播
D.$C$ 点处质元的弹性势能在增大
|
B
|
|
关于波长的正确说法是()。
A.同一波线上,相位差为 $2 \pi$ 的两个质元间的距离
B.同一波线上,振动状态相同的两点之间的距离
C.在一个周期内波所传播的距离
D.两个波峰(或波谷)的距离
|
C
|
|
下列说法正确的是()。
A.波速表达式 $u=\lambda v$ ,则波源频率越高,波速越大
B.横波是沿水平方向振动的波,纵波是沿竖直方向振动的波
C.机械波只能在弹性介质(媒质)中传播,而电磁波可以在真空中传播
D.波源振动的频率就是波的频率,波源振动的速度就是波的传播速度
|
C
|
|
驻波中相邻两波节之间各点,在振动时相同的是()。
A.频率
B.相位
C.振幅
D.振动速度
|
A
|
|
电磁波在空间传播时,某时刻在空间某点处,电场强度 $E$和磁场强度 $H$ 相同的是( )。
A.频率
B.相位
C.振幅
D.振动方向
|
D
|
|
用劈尖干涉检验工件的表面,当波长为 $\lambda$ 的单色光垂直人射时,观察到干涉条纹如图12-1所示,图中每一条条纹弯曲部分的顶点恰好与右边相邻的直线部分相切,由图可判断出工件表面 ( )。
A.有一凹陷的槽,深为 $\frac{\lambda}{4}$
B.有一凹陷的槽,深为 $\frac{\lambda}{2}$
C.有一凸起的梗,高为 $\frac{\lambda}{2}$
D.有一凸起的梗,高为 $\frac{\lambda}{4}$
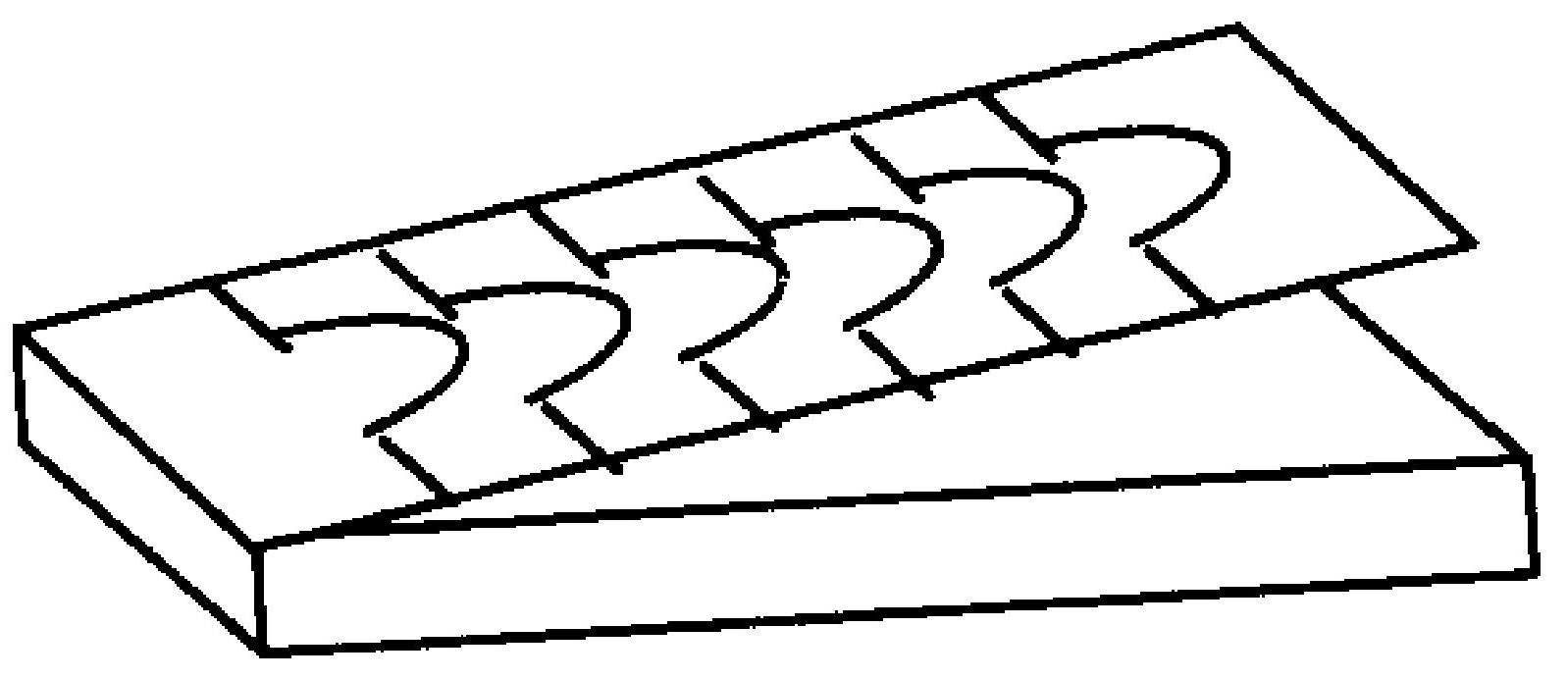
图 12-1
|
B
|
|
严格地讲,空气折射率
大于 1 ,因此牛顿环实验中若将玻璃夹层中的空气逐渐地抽去而成为真空时,牛顿环条纹将()。
A.变大
B.缩小
C.不变
D.消逝
|
C
|
|
月球距地面约 $3.86 \times 10^{8} \mathrm{~m}$ ,月光的中心波长 $\lambda=550 \mathrm{~nm}$ ,若用直径 $D=5.0 \mathrm{~m}$ 的天文望远镜观察月球,则所能分辨月球表面上的最小距离为()。
A. 1.2 m
B. 5.1 m
C. 51.2 m
D. $5.1 \times 10^{4} \mathrm{~m}$
|
C
|
|
图12-2中所示的 $X$ 射线束不是单色的,而是含有从 0.90 $\times 10^{-10} \mathrm{~m}$ 到 $1.40 \times 10^{-10} \mathrm{~m}$ 范围内的各种波长,晶体的晶格常数 $d =2.75 \times 10^{-10} \mathrm{~m}$ ,则可以产生强反射的 $X$ 射线的波长是()。
A. $1.38 \times 10^{-10} \mathrm{~m}$
B. $1.19 \times 10^{-10} \mathrm{~m}$
C. $0.95 \times 10^{-10} \mathrm{~m}$
D. $0.92 \times 10^{-10} \mathrm{~m}$
E.以上均不对
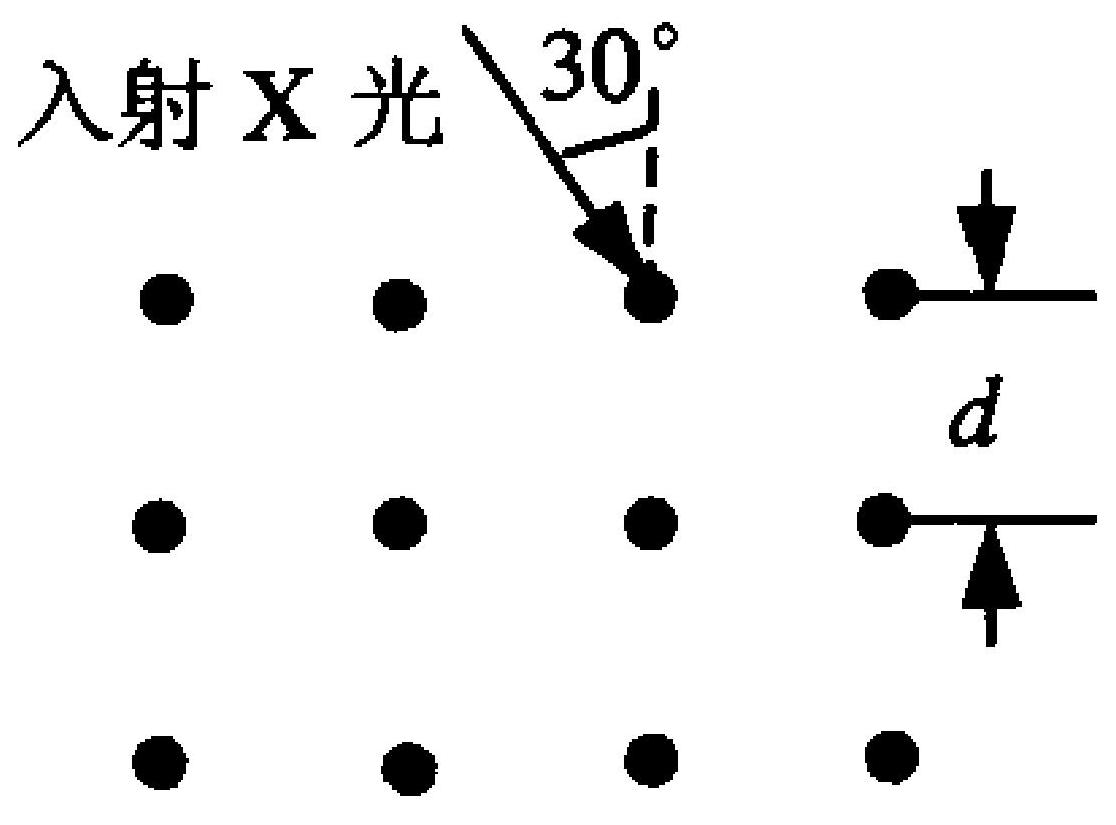
图 12-2
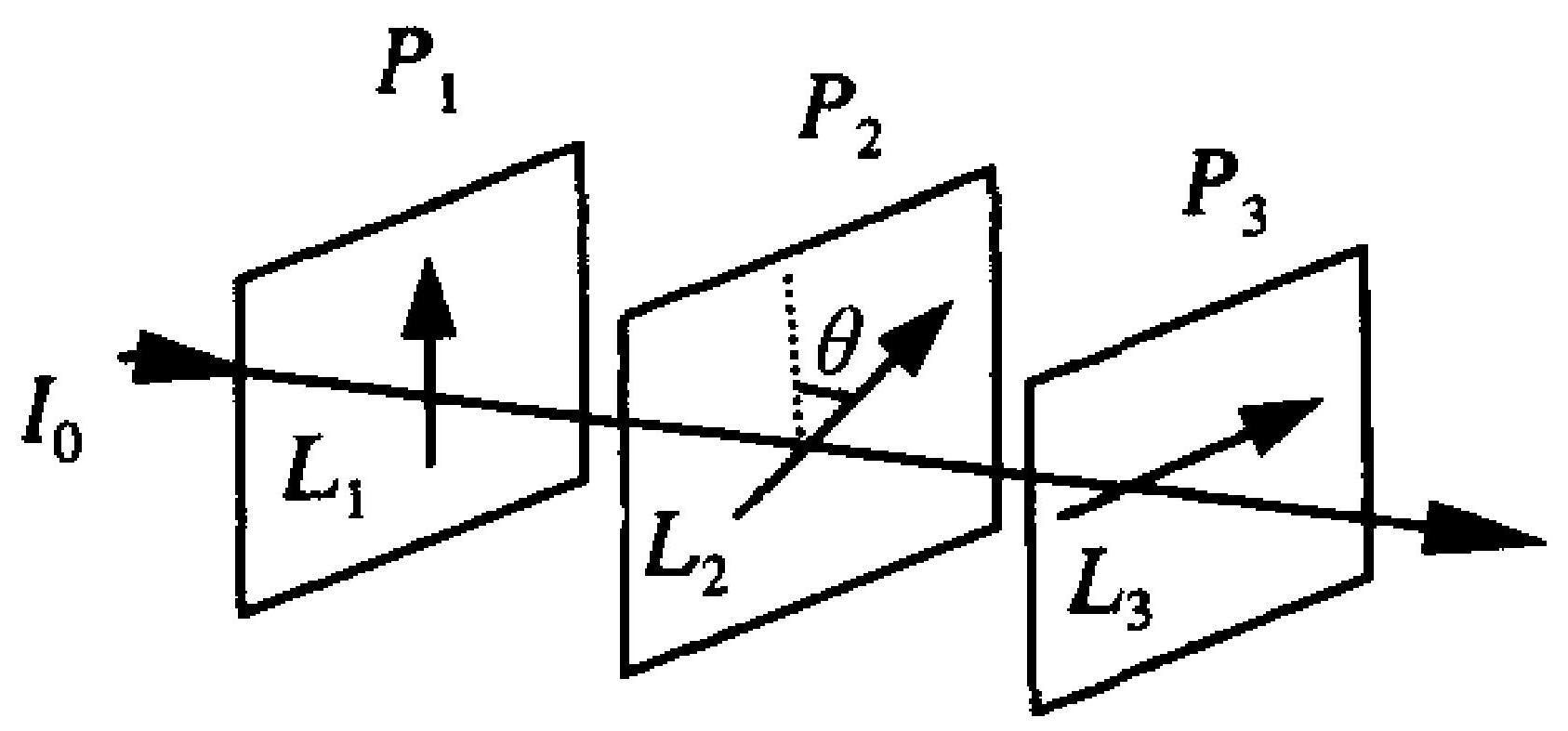
图 12-3
|
B
|
|
三块偏振片 $P_{1}, P_{2}, P_{3}$ 平行地放置(图12-3),$P_{1}$ 的偏振化方向和 $P_{3}$ 的偏振化方向相互垂直,一束光强为 $I_{0}$ 的平行单色自然光垂直地射到偏振片 $P_{1}$ 上,若每个偏振片吸收 $10 \%$ 的人射光,当旋转偏振片 $P_{2}$ 时(保持其平面方向不变),则通过偏振片 $P_{3}$ 的最大単强为 。
A. $0.091 I_{0}$
B. $0.101 I_{0}$
C. $0.0455 I_{0}^{\circ}$
D. $0.364 I_{0}$
|
C
|
|
如图12-4所示,在单缝衍射实验中,若将缝宽 $a$ 稍稍加大些,同时使单缝沿 $y$ 轴方向向上作微小位移,则屏 $C$ 上的中央亮纹将 。
A.变窄,同时向上移
B.变窄,同时向下移
C.变宽,同时向上移
D.变宽,同时向下移
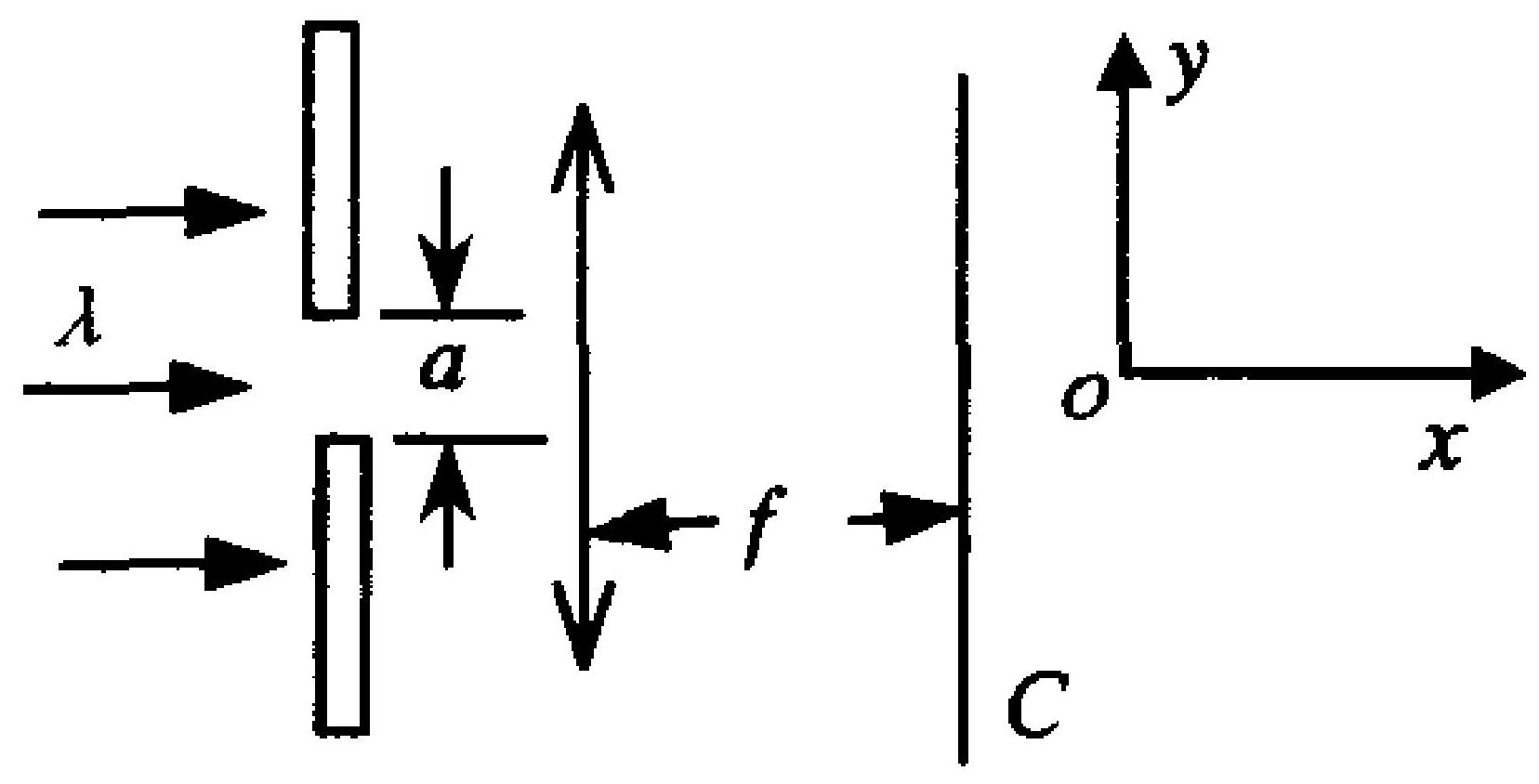
图 12-4
E.变窄,不移动
F.变宽,不移动
|
C
|
End of preview. Expand
in Data Studio
No dataset card yet
- Downloads last month
- 10